A "New" Special Point in a Triangle.

Question

I was playing with the software Geometry Expressions and I was exploring generalizations of special points in triangles (centroid, orthocenters, etc.) when I stumbled upon this construction.

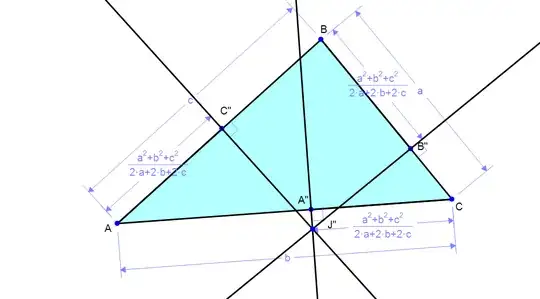
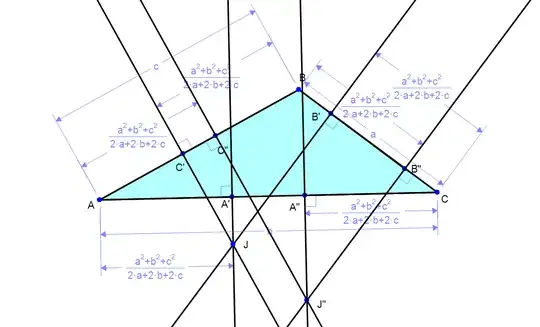
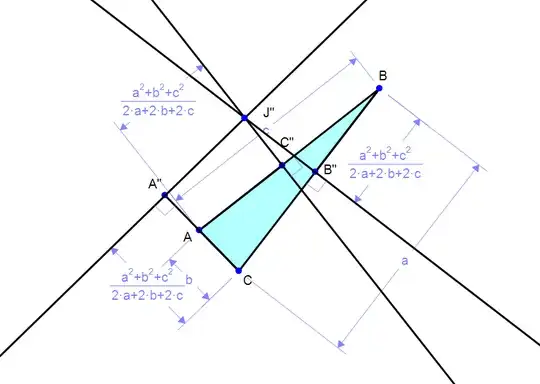
J is always located at the intersection of the three lines but can either be inside or outside the triangle depending upon its shape. If one positions A",B",C" at the critical distance from C,B, A, one can construct a second point J".

J and J'on the same figure:

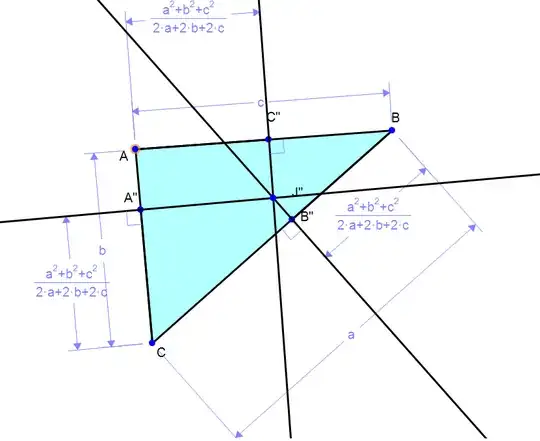
Different triangles, with J inside or outside:

Proof:

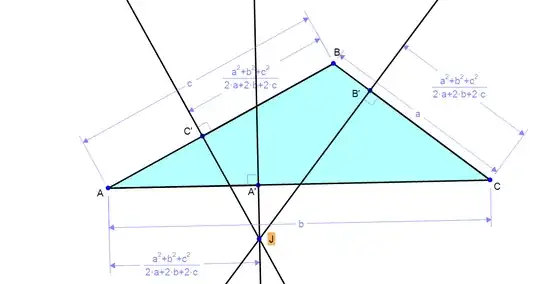
The way I constructed the point J: Position A',B',C' such that: $$ \overrightarrow{CA'} =k \overrightarrow{CA} $$ $$ \overrightarrow{BB'} =k \overrightarrow{BC} $$ $$ \overrightarrow{AC'} =k \overrightarrow{AB} $$

Define J: $$ \overrightarrow{BC'} . \overrightarrow{C'J} =0 $$ $$ \overrightarrow{AA'} . \overrightarrow{A'J} =0 $$ $$ \overrightarrow{BB'} . \overrightarrow{B'J} =0 $$

Solve for k and find: $$ k= \frac{ a^{2} +b^{2}+c^{2}}{2a+2b+2c} $$

Properties

Following "MyMolecule"'s hint, O, circumcenter of the triangle is the midpoint of JJ".(A is not on the line). The software returns for the distance OJ: $$OJ=\dfrac{\sqrt{a}\cdot \sqrt{b}\cdot \sqrt{-c^{5}+c^{4}\cdot (2\cdot a+2\cdot b)+c^{3}\cdot \left (-2\cdot a^{2}-a\cdot b-2\cdot b^{2}\right )+c^{2}\cdot \left (2\cdot a^{3}-a^{2}\cdot b-a\cdot b^{2}+2\cdot b^{3}\right )+c\cdot \left (-a^{4}+2\cdot a^{3}\cdot b-2\cdot a^{2}\cdot b^{2}+2\cdot a\cdot b^{3}-b^{4}\right )}}{(a+b+c)\cdot \sqrt{(a+b-c)\cdot (a-b+c)\cdot (-a+b+c)}}$$

Let I be the incenter. A", B' are concyclic and both belong to the circle of center I. More generally, the center of any circle passing through A", B' is located on the line IC.

Have J,J' ever been named in classical geometry?

Is there a theory about all the points that can be constructed with a straight edge and a compass out of a triangle (intersection of three lines, three circles, etc.)?

Answer 1

Look at this picture. As said in one of my comments, it is fruitful to consider the issue in a reverse manner : is it possible that an interior point $P$ with pedal triangle $A'B'C'$ be such that (red line segments in the figure below) :

$$\underbrace{AB'=BC'=CA'}_{=x} \ \ ?$$

The answer is that, if such an $x$ exists, necessarily, its value is :

$$x=\frac{a^2+b^2+c^2}{2(a+b+c)}\tag{1}$$

The proof is easy : applying 3 times the equality of 3 hypotenuses of right triangles (dotted lines), we get

$$\begin{cases}x^2+d_3^2&=&(a-x)^2+d_1^2\\ x^2+d_1^2&=&(b-x)^2+d_2^2\\ x^2+d_2^2&=&(c-x)^2+d_3^2\\\end{cases}$$

Adding these 3 equations, after different cancellations, we get a first degree equation for $x$ whose solution is (1).

Remarks :

1. This proof is as well valid if point $P$ is situated outside triangle $ABC$.

2. One could say that his proof is an analytical equivalent to the proof given by Shaktyai.

The fact that (1) is also a sufficient condition deserves a proof of its own. I will not do it. Let me plainly say that it looks a not-too-difficult task by using the barycentric (or trilinear) coordinates one finds in the reference given by Blue for the so-called "Laemmel points" $P(44)$ and $U(44)$.