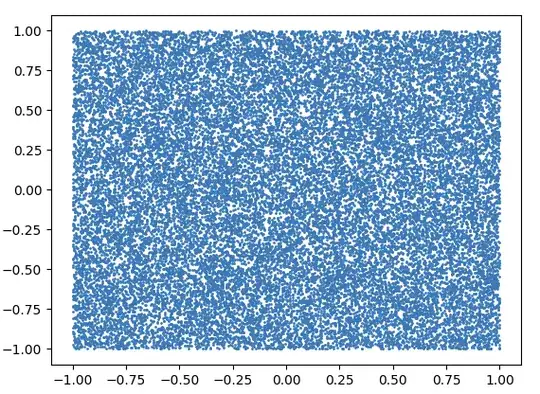
I am drawing points uniformly in a hypercube $x \in [-1,1]^n$ and I would like to find a map f(x) = y such that $||y||_1 \leq 1$ and that the uniform distribution is conserved.
My own attempt at this basically rescales the vector x, to the appropriate length, but preserves the direction.
$y = \frac{||x||_\infty}{||x||_1} x$
Written in python it looks like this:
def hypercube_to_simplex(x):
c = np.max(np.abs(x),axis=1) / np.linalg.norm(x, ord=1,axis=1)
y = c[:,None] * x
return y
X = np.random.rand(30000,2)*2-1
plt.scatter(X[:,0],X[:,1],s=1)
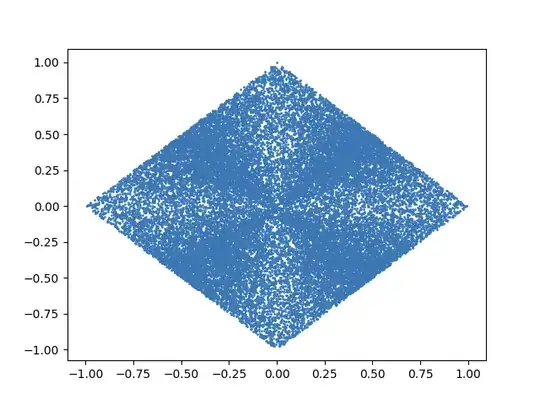
Y = hypercube_to_simplex(X)
plt.figure()
plt.scatter(Y[:,0],Y[:,1],s=1)
The problem with my method is that it does not preserve the uniform distribution as seen by the scatter plots:
To me it looks like I need to skew the distribution of each individual $x_i$, but I can't quite grasp how. I know this question is related to previous questions asked like: Uniform sampling of points on a simplex but I can't figure out how to apply the solutions from there to my problem.