0

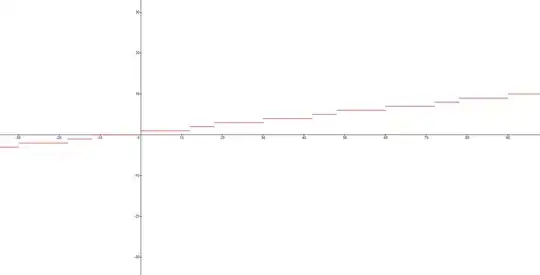
Question. How can we prove that this function is non-decreasing?

Graph of the function

That is:

$$ f: \Bbb{R} \to \Bbb{Z} \\ f(x) = [\frac{x}{1}] - [\frac{x-1}{2}] - [\frac{x - 1}{3}] - [\frac{x - 2}{3}] - [\frac{x - 1}{5}] - [\frac{x - 4}{5}] \\ + [\frac{x - 1}{6}] + [\frac{x - 5}{6}] + [\frac{x-1}{10}] + [\frac{x - 9}{10}] + [\frac{x - 1}{15}] + [\frac{x-4}{15}] + [\frac{x - 11}{15}] \\ - [\frac{x - 1}{30}] - [\frac{x - 11}{30}] - [\frac{x - 19}{30}] - [\frac{x - 29}{30}] $$

or more compactly:

$$ f(x) = \sum_{d \mid p_3\#}(-1)^{\omega(d)}\sum_{0 \leq r \lt d \\ r^2 = 1 \pmod d}\left\lfloor \frac{x - r}{d}\right\rfloor $$

By this very elegant MSE answer: obviously there is a trend line, and the slope of this trend line can be computed as:

$$ m = \sum_{d\mid p_3\#} \frac{(-1)^{\omega(d)}|H_d|}{d} $$

where $H_d = \{r \in \Bbb{Z} : 0 \leq r \lt d \ \wedge \ r^2 = 1 \pmod d\}$. It is known that $H_d$ is precisely the set of standard residues of a subgroup of $(\Bbb{Z}/d)^{\times}$, namely the subgroup of all $x \in \Bbb{Z}/d$ that square to $1$ modulo $d$.

Daniel Donnelly
  • 22,288
  • 1
    Note that $f(x) - mx$ is periodic with a period of 30 – Command Master Sep 21 '23 at 04:01
  • @CommandMaster how did you come to that conclusion so quickly? Did you expand floor using the modular arithmetic formula? Also I'm not quite seeing how that helps us. Could you elaborate some in an answer? – Daniel Donnelly Sep 21 '23 at 04:07

1 Answers1

1

A more general number-theoretic answer:

Note that $f(x)$ only changes at integers. $$f(n + 1) - f(n) = \sum_{d | p_3 \#} {(-1)^{\omega(d)} \sum_{0\leq r< d\\r^2\equiv 1\pmod d} \lfloor\frac{n+1-r}d\rfloor - \lfloor\frac{n-r}d\rfloor} = \sum_{d | p_3 \#} {(-1)^{\omega(d)} \sum_{0\leq r< d\\r^2\equiv 1\pmod d} [n+1\equiv r \pmod d]} = \sum_{d | p_3 \#} {(-1)^{\omega(d)} [(n+1)^2\equiv 1 \pmod d]} = \sum_{d | p_3 \#} {(-1)^{\omega(d)} \prod_{p | d}[(n+1)^2\equiv 1 \pmod p]} = \sum_{d | p_3 \#} {\prod_{p | d}- [(n+1)^2\equiv 1 \pmod p]} = \prod_{p | p_3\#} {1 - [(n+1)^2\equiv 1 \pmod p]}$$

Which is obviously nonnegative.

Old solution:

Note that $\lfloor \frac{x - r}{b} \rfloor = \frac{x - r - (x-r\mod b)}{b} = \frac{x-r-((x\mod b) - (r\mod b) \mod b)}{b}$, so $\lfloor \frac{x - r}{b} \rfloor - \frac{x}{b}$ is periodic with period $b$. Because $f(x) - mx$ is a sum of terms each with a period dividing $30$, $f(x) - mx$ is periodic with period $30$.

We'll show that if $f(x)$ is non-decreasing for $0 \leq x < 60$, then it must be non-decreasing in general.

Suppose $x < y$, and we'll show $f(x) \leq f(y)$. Due to the periodicity $f(x) \leq f(y)$ iff $f(x + 30k) \leq f(y + 30k)$, so we can assume $0 \leq x < 30$.

We will use induction on $\lfloor \frac y{30} \rfloor$. As a base case, if $y < 60$ then $f(x) \leq f(y)$ follows by our assumption of $f$ not decreasing in the range $0 \leq x < 60$. Otherwise $x < y - 30$, and by induction $f(x) \leq f(y - 30)$, but due to the periodicity $f(y - 30) = f(y) - 30m < f(y)$, so $f(x) < f(y)$.

To show it's non-decreasing in the range, since the function only changes at integers, we can just evaluate it for the entire range, or look at the graph.

Command Master
  • 1,429
  • 1
    Note that while this is a valid answer, it doesn't generalize well to other $p_n, n\gt 3$ because we would need to inspect the graphs of each. – Daniel Donnelly Sep 21 '23 at 05:11
  • 1
    @MathCrackExchange true. To do that you'd need a more number-theoretic approach – Command Master Sep 21 '23 at 05:12
  • What a beautiful proof of the general case! See https://math.stackexchange.com/questions/4772866/this-alternating-sum-of-fractional-floor-functions-over-the-divisors-of-primoria for another potential proof.

    In fact, I recommend that you edit this post, copy / paste over your general case proof to that newer post. That will give you two answers receiving upvotes and also you already answered this one perfectly!

     – Daniel Donnelly Sep 21 '23 at 15:22