Is $|1+x| \ge 1 - |x|$ true for all $x$?
When I solve this problem myself, I solved that it's true for all $x$.
But when I put it into Desmos, I get this: https://www.desmos.com/calculator/vgxm3q1fso, and tells me that when $-1 < x < 0$, there's no solution
Then when I go to Wolfram Alpha, I get that it's true for all $x$.
Could someone please tell me what's going on?
Thanks!
You and Wolfram Alpha are correct, the solution should be the whole plane. I've reported the issue to Desmos and got a quick feedback:
Thanks for reaching out about this. It's a limitation of our implicit plotter.
You're absolutely right that the solution set for that inequality should be the whole plane. The problem is the exact equality on the boundary. The way our implicit plotter works in cases like this is to sample lots of points in the plane, evaluate them in (a normalized version of) your expression, and check the sign. We detect boundaries by looking for places where the sign flips. The problem with the non-strict inequality is, at exactly -1, we don't detect a sign change, so we miss the region on the other side of the boundary.
I know that seems simple enough to correct: just add an additional check for exact equality. The problem with that approach is that it works for integers, but as soon as you introduce decimal values, floating-point rounding error means that the boundary would splinter into lots of little pieces because of numerical instability. So, unfortunately, you're just running into a bad case for our implicit plotter here: we can only find boundaries between regions with different signs.
I know that's not a totally satisfying answer, but hopefully it gives you a bit of an idea why you're running into this problem. The general problem is probably not something we're going to solve soon, but we definitely appreciate you reaching out about it.
Clearly $|1+x|\geq1-|x|$, and even Desmos agrees with this if you do not consider the inequality in one line.
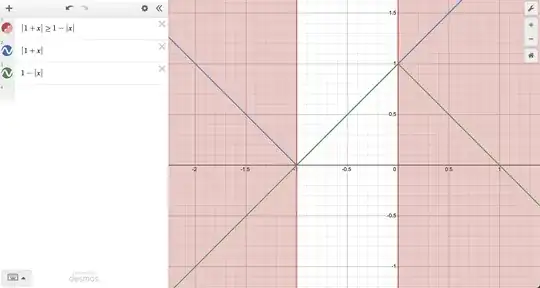
Similar to @user317176's comment, I believe Desmos is mixing up equality and strict inequality as is evident below with a simpler case:
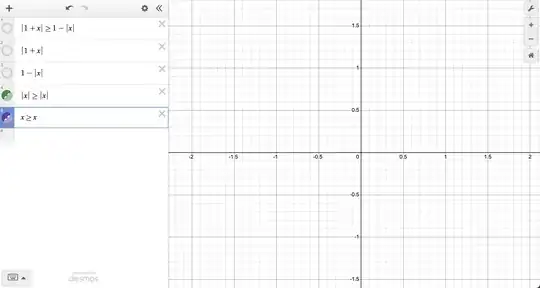
My guess: I think Desmos does not include $-1<x<0$ because I think it changes each inequality into parts. When I say this, I mean it takes an inequality and somehow turns it into an equation (probably for computational reasons). I believe this because $x=x$ does not show anything, which indicates a connection between inequalities and equations, specifically when they are exactly equal to each other.
The following shows how $x=x$ does not produce an output, even though we expect the entire plane filled as every $x$ satisfies the equation.
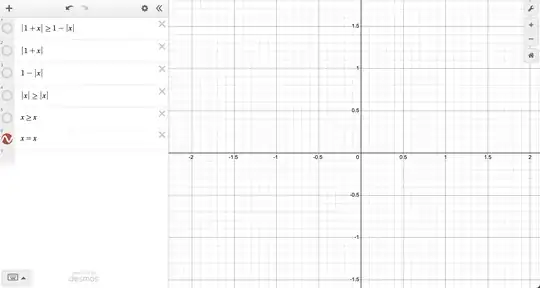
I am no expert at Desmos, but I strongly believe that this is a problem with Desmos, so I would email them to fix it or ask on another Stack Exchange website.
The desired inequality is equivalent to $$|x-(-1)|+|x-0|\ge 1,$$ which we can interpret on the number line as saying that the sum of distances from $-1$ and $0$ is at least $1$. This is clear for $x\le -1$ and for $x\ge 0$. For $-1\le x \le 0$, the sum is exactly $1$.
An alternative approach is to minimize $|1+x|+|x|$, which you can do via linear programming by minimizing $y+z$ subject to linear constraints \begin{align} y&\ge 1+x \tag1\label1 \\ y&\ge -(1+x) \tag2\label2 \\ z&\ge x \tag3\label3 \\ z&\ge -x \tag4\label4 \end{align} Adding \eqref{1} and \eqref{4} yields $$y+z\ge (1+x)+(-x) = 1,$$ as desired.
More succinctly, $$|1+x|+|x|\ge (1+x)+(-x) = 1.$$
