1

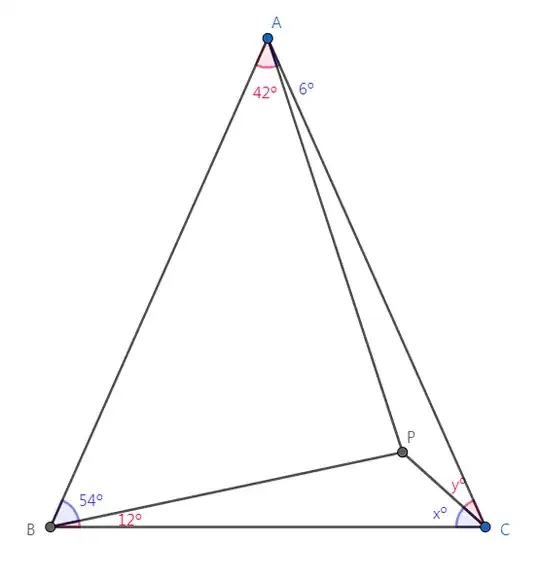
In triangle $ABC$, $P$ is point such that $\angle PAB = 42^{\circ}$, $\angle PBA = 54^{\circ}$, $\angle PAC = 6^{\circ}$, $\angle PBC = 12^{\circ}$. Find $ \angle PCB$.

enter image description here

I found the $ \angle PCB = 42^{\circ} $ , from Geogebra

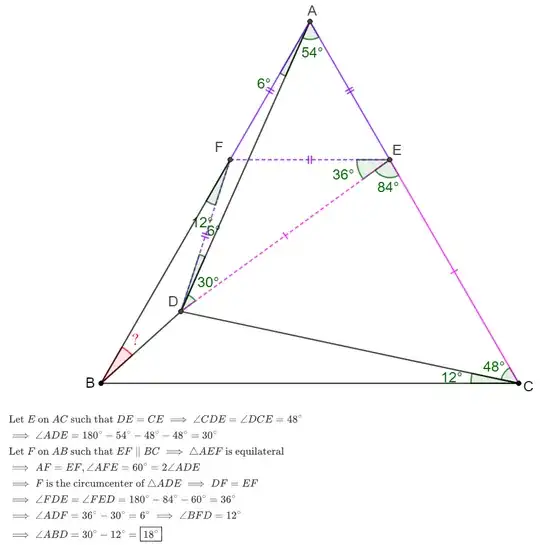
But I want to solve this problem using Synthetic or Trigonometry.

Someone solved this problem before when it was an equilateral triangle, but in this case it is difficult to solve because it is an isosceles triangle. Link: Conjecture about a point inside an equilateral triangle divided by integer angles

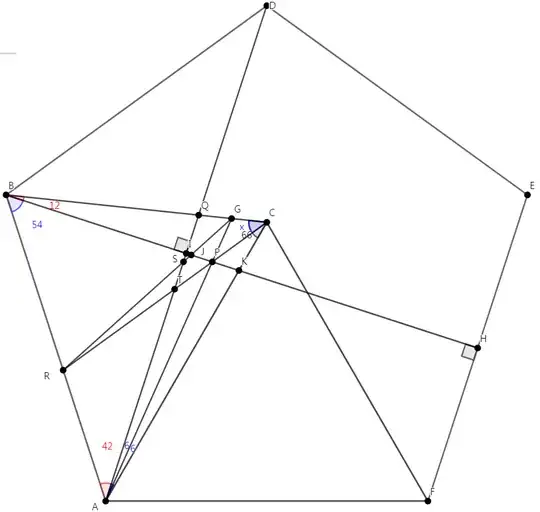
This is the process of solving problems through drawing with @dfnu ideas.

enter image description here

Using regular pentagons and equilateral triangles, we can create the isosceles triangle and angles we are looking for. I think the proof will be complete when $\square ACGR $ shows an inscribed rectangle.

dfnu
  • 8,050
Snupi
  • 151
  • 1
    Diagram would be good. – coffeemath Sep 14 '23 at 16:06
  • 1
    Please share with us what you've tried. – dfnu Sep 15 '23 at 09:05
  • I just drew and measured the angle using a protractor. It's embarrassing to even call it trial. – Snupi Sep 15 '23 at 09:10
  • Those angles make me think of a regular pentagon. For example: if inside a regular pentagon you draw an equilateral triangle (sharing one side with the pentagon) at both sides you end up with two isosceles triangles of your kind. – dfnu Sep 15 '23 at 09:37
  • Hint: the title of your question. – jjagmath Sep 15 '23 at 10:41
  • @dfnu A regular pentagon has only 36, 72, 108 degrees. Where do we find the isosceles triangle of 66 degrees? – Snupi Sep 15 '23 at 14:32
  • As I said, construct the equilateral triangle internal to the pentagon and sharing with it one side. Connect now the triangle vertex with the other vertices of the pentagon... – dfnu Sep 15 '23 at 15:36
  • @dfnu With your wise suggestions, I think I can complete this problem using only the Construction. But I'm having a hard time finishing it. Would you help me? – Snupi Sep 16 '23 at 15:41
  • That's interesting. I will give it a try and see if I come up with some more steps! – dfnu Sep 16 '23 at 16:27

3 Answers3

4

enter image description here

I think you are on the right track, now. To complete the proof, note first that $\triangle APQ$ is isosceles, with $\measuredangle PQA = \measuredangle PAQ = 6^\circ$. Therefore $\triangle BPQ \cong \triangle BCQ$ by ASA criterion. This in turn implies that $\square BPCQ$ is cyclic, with two opposite equal sides, hence an isosceles trapezoid. So $PC\parallel BQ$, from which you get your result, that is $\measuredangle BCP = \measuredangle CBQ = 42^\circ$.

dfnu
  • 8,050
  • I am impressed by your concise explanation, and I will learn something today as well. – Snupi Sep 17 '23 at 13:06
  • @Snupi In this kind of exercises it is sometimes useful to try a sort of "reverse engineering", and figure out where the construction comes from. Of course trigonometry gives you a correct relationship, which is, however, not always straightforward to solve. – dfnu Sep 17 '23 at 19:08
3

This problem can be resolved using elementary geometry induction as following:

enter image description here

Adventitious Angles Qs Poster
  • 1,045
2

By the trigonometric corollary of Ceva's theorem:

$$\frac{\sin(54^\circ)}{\sin(12^\circ)}\cdot\frac{\sin(6^\circ)}{\sin(42^\circ)}\cdot\frac{\sin(x)}{\sin(y)} = 1$$ And by the angle sum of a triangle, $$x+y = 66^\circ$$

$$\frac{\sin(x)}{\sin(66^\circ - x)} = \frac{\sin(12^\circ)\cdot \sin(42^\circ)}{\sin(54^\circ)\cdot \sin(6^\circ)}$$

Now this simplifies very easily if you know the compound angle identities and the trigonometric ratios for $18^\circ$ and $30^\circ$. With those identities and after multiplying by $\frac{\sin(24^\circ)}{\sin(24^\circ)}$ we get

$$ \begin{align}\frac{\sin(x)}{\sin(66^{\circ} - x)} &= \frac{\sin(42^\circ)[\sin(30^\circ) + \sin(18^\circ)]}{\cos(36^\circ)\sin(24^\circ)} \\ &=\frac{\sin(42^\circ)}{\sin(24^\circ)} \end{align} $$ Thus, $$ \frac{\sin(x)}{\sin(66^\circ - x)} = \frac{\sin(42^\circ)}{\sin(24^\circ)} $$

As a consequence, one apparent solution is $x=42^{\circ}$ which can be shown to be the only one by noting that $\frac{\sin x}{\sin(66^{\circ} -x)}$ is injective on $[0, 66^{\circ})$.

Sahaj
  • 5,355
  • Your kindness will be remembered for a long time. – Snupi Sep 15 '23 at 14:02
  • 1
    I'm glad to help, but next time do try to provide more context/attempts on your problems in order to get help faster. – Sahaj Sep 15 '23 at 14:14
  • 1
    May be you could observe that $\frac{\sin(x)}{\sin(66^\circ-x)}$ is increasing for $x \in [0^\circ, 60^\circ)$ to justify the conclusion. – jjagmath Sep 15 '23 at 15:18