0

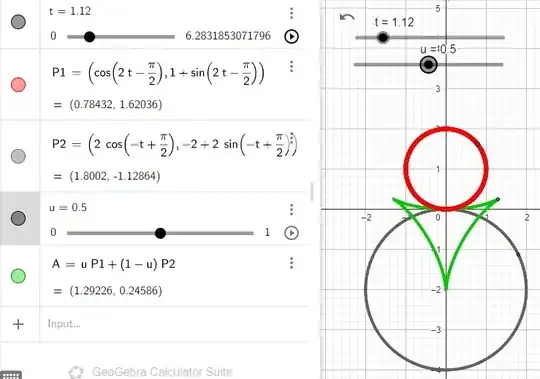
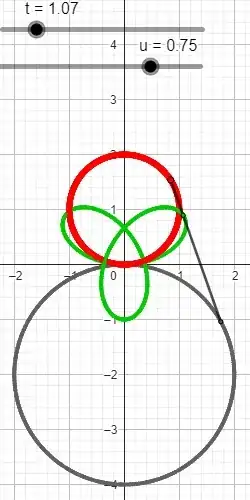
A mechanical device consists of two circular gears, one of radius 2 centered at (0, −2) and the other of radius 1 centered at (0, 1). The gear of radius 2 rotates clockwise at unit angular velocity (1 radian per second), while the gear of radius 1 rotates counterclockwise without slipping at the contact point. The two gears each carry a small peg on their circumference, and these pegs are connected together by an elastic band. Initially, both pegs are at the origin

a) Write parametric equations for the motion of the midpoint P of the elastic band. (Use vectors; begin by expressing the position vector in terms of simpler vectors, then express each of them in terms of t).

b)Express the velocity of the point P as a function of t. Calculate the velocity and the acceleration at t = 0.

I was trying to first get the parametric equations of both gears:

gear of radius 2:

$$x(t) = 2cost$$ $$y(t) = 2sint - 2$$

gear of radius 1:

$$x(t) = cost$$ $$y(t) = sint + 1$$

the get some vector from some point in the circumference of gear 1 to some point in the circumference of gear 2 we subtract his x and y componets, then divide by half to get the midpoint is this correct?

$$P = \frac{(2cost-cost, 2sint-2-(sint+1))}{2}$$

VOZ ESTOICA
  • 101

2 Answers2

1

(see animated Geogebra picture here : take $u=\tfrac12$).

Question a) :

Pegs' coordinates can be written in this way :

$$P_1=\pmatrix{0\\1}+ \pmatrix{\sin(\color{red}{2}t-\alpha)\\-\cos(\color{red}{2}t-\alpha)} \ \text{with time shift} \ \alpha=-\pi/2 $$

$$P_2=\pmatrix{0\\-2}+\pmatrix{-\color{blue}{2}\sin(t-\beta)\\-\color{blue}{2}\cos(t-\beta)} \ \text{with time shift} \ \beta=+\pi/2$$

Please note that the red $\color{red}{2}$s accounts for the ratio $2:1$ of angular speeds, whereas the blue $\color{blue}{2}$s (intended pun) account for the ratio of the corresponding wheels' radii, these ratio being inverse one of the other.

The former equations can be transformed into

$$P_1=\pmatrix{\sin(2t)\\1-\cos(2t)} \ \text{and} \ P_2=\pmatrix{-2\sin(t)\\-2-2\cos(t)}$$

finally giving the parametric equations of their midpoint :

$$A=\pmatrix{-\sin(t)+\tfrac12\sin(2t)\\-\cos(t)-\tfrac12 \cos(2t)-\tfrac12}=-\pmatrix{\sin(t)\\\cos(t)}+\tfrac12 \pmatrix{\ \ \sin(2t)\\-\cos(2t)}+\pmatrix{0\\-\tfrac12}$$

which is the locus of a point situated on the border of a disk of radius $1/2$ rolling inside a disk of radius $1+1/2=3/2$ (plus a final translation), a classical description of a deltoid (see for example here).

We are fortunate enough to live in a time where graphical tools (public domain software like Geogebra, Desmos, etc) are available as an efficient mean to check our hypotheses, help us to make conjectures etc.

Here is what I have done with Geogebra in a short amount of time :

enter image description here

The midpoint is obtained by taking $u=\frac12$ in relationship $A=uP_1+(1-u)P_2$. The result (green curve described by midpoint $A$) is visibly a deltoid curve.

Funnily, when one changes $A=\frac{P_1+P_2}{2}$ into $A=\frac{3P_1+P_2}{4}$ ($u$ changed from $1/2$ to $3/4$), one gets a trefoil knot curve instead. Not surprising when one knows the representation of a (3D) trefoil knot as :

$$\begin{cases}x&=&\sin t + 2 \sin 2t\\ x&=&\cos t - 2 \cos 2t\\ z&=&-\sin 3t \end{cases}$$

Experiment other values of $u$ like $2/3$ !

enter image description here

Jean Marie
  • 88,997
  • why is P1+P2 instead of P2- P1? – VOZ ESTOICA Sep 11 '23 at 14:09
  • can you also explain the phase shift in both gears – VOZ ESTOICA Sep 11 '23 at 14:30
  • First question : the midpoint of two points has coordinates the arthmetical mean of the coordinates $(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})$ symbolized by $\frac{P_1+P_2}{2}$ which is a point, whereas $P_2-P_1$ is a vector, $\vec{P_1P_2}$. – Jean Marie Sep 11 '23 at 16:01
  • Second question about the time shift : Let $O_1=(0,1), O_2=(0,-2)$ be the centers of the wheels. At starting time, when $t=0$, peg $P_1$ is such that $\vec{O_1P_1}$ is directed plain south, i.e., corresponds to $-\pi/2$ (explaining the $2t-\pi/2=-\pi/2$ when we take $t=0$), whereas peg $P_2$ is such that $\vec{O_2P_2}$ is directed plain north i.e., corresponds to $+\pi/2$ (explaining the $-t+\pi/2=+\pi/2$ when we take $t=0$). Besides, I am sure you have understood that the "minus" sign in front of $t$ accounts for the counterclockwise movement. – Jean Marie Sep 11 '23 at 16:14
  • Thank you, very nice explanation – VOZ ESTOICA Sep 11 '23 at 16:29
1

Calling

$$ \cases{ p_1 = -i r_1\\ p_2 = i r_2\\ \phi_1=\frac{\pi}{2}\\ \phi_2=-\frac{\pi}{2}\\ r_1=2\\ r_2=1\\ \omega_1=1\\ \omega_2 = -\frac{r_1}{r_2}\omega_1 } $$

we have

$$ z = \frac 12\left(p_1+p_2+r_1 e^{i\omega_1 t+\phi_1}+r_2 e^{i\omega_2 t+\phi_2}\right)=-\left(\sin t+\frac 12\sin(2t)\right)+i\left(\cos t-\frac 12\cos(2t)-\frac 12\right)= x + i y $$

enter image description here

Cesareo
  • 36,341