Bisecting an angle with a right-angled bent ruler (that can coordinate the vertex and both edges)

Question

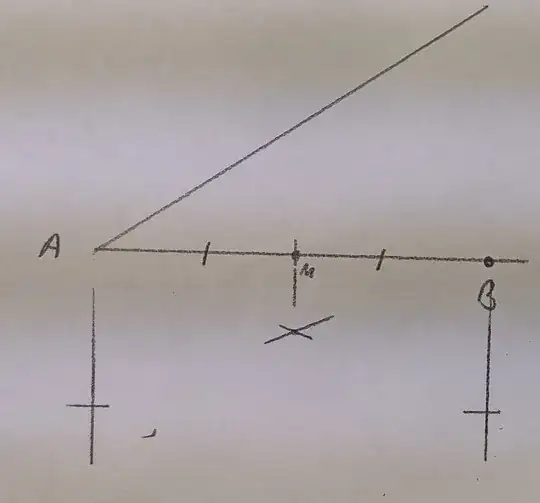
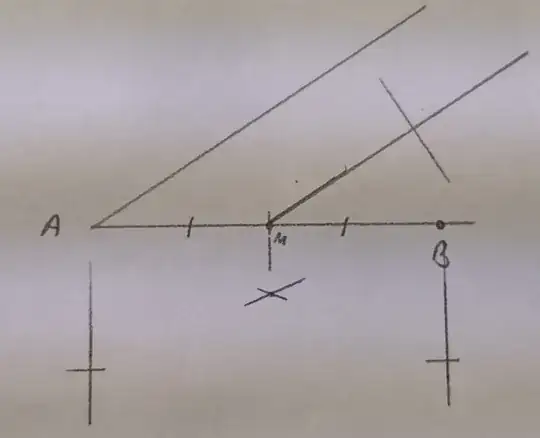
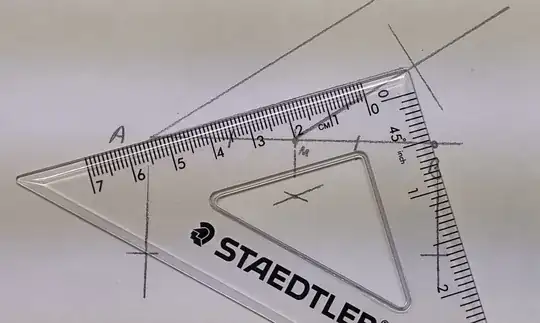
This thesis claims that you can construct any point constructible with ruler and compass with only a "bent ruler" -- that is, a pair of moveable rays joined at a specific angle.

"Euclidean constructions: alternate tools to the traditional compass and straightedge" by Sandra Kay Birrell, California State University, 1983

However it does not provide constructions themselves with bent rulers. It seems with specifically a right-angled ruler (where the angle between the two rays is a right angle) it is quite difficult to bisect an angle. How can it be done?

(Note that this is a different question to the existing similar one on Math Stack Exchange, as the other one explicitly excludes the ability to coordinate the vertex and the two rays simultaneously.)

Answer 1

First, on one of the rays of the angle, plot a point so you have a segment. Then bisect that segment. (This can be done by constructing a rectangle and its diagonals, then dropping a perpendicular from the intersection of the diagonals.)

Then, construct a ray parallel to the other ray of the angle through point M. (This is done by constructing a perpendicular to that ray, and then another to that one through M.)

Now we can use the technique you mentioned. Because M is the midpoint of A and B, it is also the center of the circle containing diameter AB. Thus, using Thales' Theorem, we can say that the right triangle formed by the bent ruler is inscribed in semicircle AB, and thus the right angle's vertex is the same distance from M.

Since we've now essentially created a parallelogram with two congruent consecutive sides, it's a rhombus, and thus the diagonal will bisect the angle. Which completes the construction.