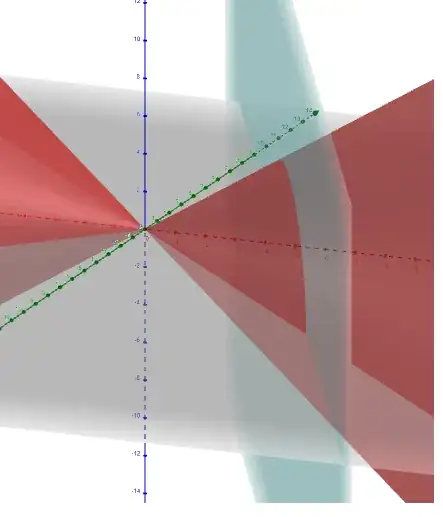
I need to find the surface area of a solid bounded by $x^2 = z^2 + (y-3)^2$ and $2x+y=12$. Once I set up the integral I can calculate it,but the problem is that I don't know how to set it up.Any help is appreciated.
Asked
Active
Viewed 78 times
-1
-
1Quick beginner guide for asking a well-received question + How to ask a good question – Sep 05 '23 at 15:50
-
1https://www.geogebra.org/3d can help to visualise the objects. – Kurt G. Sep 05 '23 at 16:37
-
The given cone is infinite. Do you have another constraint? Or is the solid the part of the cone between its vertex and the plane? – user170231 Sep 05 '23 at 16:49
-
I have only these 2 constraints – sour Sep 05 '23 at 16:52
-
@KurtG. Thank you for a link :) I didn't know it exists. – CiaPan Sep 06 '23 at 08:02
-
1@user170231 The two constraints are sufficient. When the angle between the plane and the cone axis is bigger than the angle between the axis and the generatrix (and the plane does not contain the apex), then there is a bounded solid region between the two surfaces. – CiaPan Sep 06 '23 at 08:08
1 Answers
1
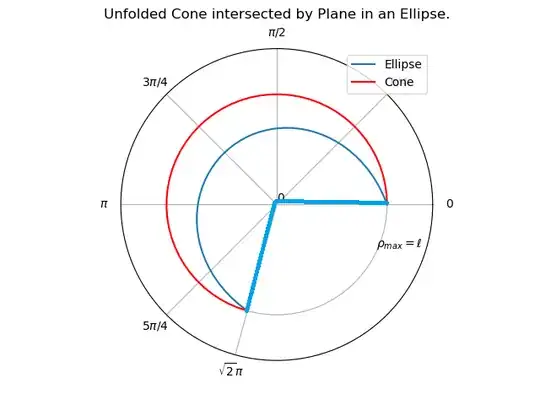
The first transformation I would make is to replace $y-3$ with $y$ which turns the equations into $$ x^2=z^2+y^2\,,\quad 2x+y=9\,. $$ Then let's rename the variables to have compatibility with this answer: $$ z^2=x^2+y^2\,,\quad 2z+y=9\,. $$ I believe that with the methods in that linked answer one can unfold the $\color{red}{\text{cone}}$ into the $\mathbb R^2$-plane and get an equation for the $\color{blue}{\text{ellipse}}$ that is the intersection of the cone and the plane $2z+y=9\,.$
By isometry of the metric $ds^2$ on the cone with the metric in $\mathbb R^2$ this should lead to the following formula for the surface area in OP: $$ A=\int_0^{\sqrt{2}\,\pi}\int_0^{\color{blue}{\rho(\varphi)}}u\,du\,d\varphi $$ where $$ \rho(\varphi)=\frac{9\sqrt{2}}{2+\sin(\varphi/\sqrt{2})}\,. $$ The area $A$ is the one inside the $\color{blue}{\text{blue}}$ contour in the second picture below.
Kurt G.
- 17,136