Showing $|\sum_{k=1}^n\frac{\sin(kx)}k|<2\sqrt{\pi}$

Question

For any real $x$ and positive integer $n$, is it true that:

$$\left|\sum_{k=1}^n\frac{\sin(kx)}k\right|<2\sqrt{\pi}\quad ?$$

Please justify.

For $x \in (0,2\pi)$, you could write it as $\int_0^x \sum_{k=1}^n \cos(kt)dt$. Not sure, but this might help. — Prahlad Vaidyanathan, Aug 26 '13 at 04:58
I was thinking about this too. But the integral is kinda messy after you sum the cosines. — user70520, Aug 26 '13 at 06:43
The best it is possible to state is: $$\left|\sum_{n=1}^N \frac{\sin(nx)}{n}\right|\leq\int_{0}^{1}\frac{\sin(\pi x)}{x},dx = 1.85194\ldots$$. — Alex Ravsky, Aug 17 '17 at 02:15

Nathaniel Bubis · Answer 1 · 2013-08-26T05:21:56.360

3

Hint:

The sum inside the absolute value is the partial sum of the Fourier series of:

$$y = \frac{\pi}{2} - \frac{x}{2}$$ Gibbs phenomenon tells you that the maximum value of the sum is: $$f(0_+) + \pi\cdot0.08949 = \frac{\pi}{2}+0.08949\pi\sim1.85<2\ll2\sqrt{\pi}$$ So, $2\sqrt{\pi}$ is a very loose bound.

edited Aug 26 '13 at 05:21

answered Aug 26 '13 at 05:16

Nathaniel Bubis

33,425

1

... a partial sum of the Fourier series of ..., you mean. – Robert Israel Aug 26 '13 at 05:17
@RobertIsrael - but of course :) fixed. – Nathaniel Bubis Aug 26 '13 at 05:18
Interesting. Too bad I don't know too much about Fourier series. Is there a more elementary approach? – user70520 Aug 26 '13 at 06:41

score 3 · Answer 2 · answered Aug 26 '13 at 05:20

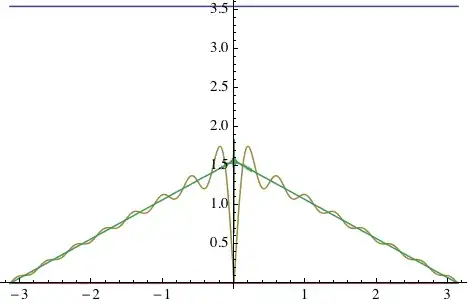
Looks like it. $|\sum_{k=1}^n\frac{\sin(kx)}k|$ is a partial sum of the Fourier series of the function $y=\frac{\pi-|x|}{2}$. Here are the sums for $n$=15 (gold) and $n$=1350 (green) along with the graph of $y=2\sqrt{\pi}$ (blue). Maybe this will help? The Gibbs effect seems to be the only thing that moves the sum anywhere towards $2\sqrt{\pi}$, but does so ever so slightly.

Showing $|\sum_{k=1}^n\frac{\sin(kx)}k|<2\sqrt{\pi}$

2 Answers2