9

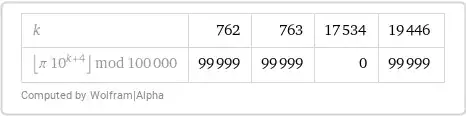
The Feynman point is a mathematical coincidence. It states that from position 762, there are six consecutive nines in the decimal expansion of pi. Some mathematical coincidences have an explanation, like Ramanujan's constant being close to an integer. Is there a known explanation for the Feynman point?

Update: the ‘special thing’ about this string of six 9s is that is occurs so early. According to Wikipedia:

For a normal number sampled uniformly at random, the probability of a specific sequence of six digits occurring this early in the decimal representation is about 0.08%. The early string of six 9's is also the first occurrence of four and five consecutive identical digits.

If we regard the strings 000000, 111111, until 999999 ‘equally important’, then we should immediately multiply this probability by 10. As with every mathematical coincidence, it could be an ‘actual coincidence’, meaning that there is no ‘explanation’. However, maybe there is in fact an ‘explanation’.

This question gives an example of a similar, but more extreme situation. In that case, there is a clear explanation.

Riemann
  • 929
  • 6
    Well, it's conjectured that $\pi$ is normal, so that in particular every finite string will appear in its decimal expansion. What's especially surprising about this particular instance? – Noah Schweber Aug 31 '23 at 20:19
  • 5
    @NoahSchweber I think the idea is that this is significantly earlier than you’d expect 6 of the same digits in a row if the digits were uniformly random (though there’s of course some implicit “p-hacking” here). – spaceisdarkgreen Aug 31 '23 at 20:32
  • 6
    I'm sure that if you studied the various expressions for $\pi$ that exhibit a regular pattern for long enough, you would be find an explanation as to why $10^{762}\pi$ was so very close to an integer. And then you could proclaim you know the reason. But I strongly doubt that this would actually spread any light on the matter. Instead, it would most likely just push the coincidence from being six $9$s in a row to being some other thing that just happened to work out. Coincidences are common. They are interesting, but seldom enlightening. – Paul Sinclair Sep 02 '23 at 02:01
  • It would help if there was a Baile-Borwein-Plouffe formula in base 10 https://en.m.wikipedia.org/wiki/Bailey–Borwein-Plouffe_formula – Riemann Sep 02 '23 at 08:32
  • That would be a BBP-type formula with b=10: https://mathworld.wolfram.com/BBP-TypeFormula.html – Riemann Sep 04 '23 at 16:12
  • Am I missing something? Speaking probabilistically about the digits of $\pi$ does not make sense ... right (especially when you speak of the probability of a number's digits occurring in exactly some decimal place)? – sreysus Sep 09 '23 at 20:20
  • Well, suppose that there would be 100 consecutive nines from position 762. Wouldn’t that be a sign that there is a higher pattern? But that is a probabilistic argument – Riemann Sep 09 '23 at 22:48
  • Thanks, I see. What about for different number systems instead of base-10? Would that lessen the probability of having 6 consecutive digits? I would assume the Feynman point would not be a special property of $\pi$, but rather a property of $\pi$ in base-10. Maybe that might give rise to some explanation. – sreysus Sep 15 '23 at 01:52
  • I checked. In base 2, there are six ones from position 11. For base 3-6, the pattern seems to be missing – Riemann Sep 15 '23 at 09:32
  • Missing from where? Also, I think it would be more suitable if you post this on MO because this is related to an unsolved problem. A question with a somewhat similar essence on MO and a website that talks about Chaitin's constant and some other examples might help. – sreysus Sep 15 '23 at 11:34
  • In base 3-6, there is no such early occurrence of six consecutive digits. – Riemann Sep 16 '23 at 09:54
  • If you search for reason within randomness, you'll leave empty-handed. You answered your own question before you even posted it: This is precisely an example of a coincidence in maths. Asking this is virtually analogous to asking why a sequence of $n$ consecutive heads appears in an infinite series of coin tosses. – Arjun Vyavaharkar May 17 '24 at 02:37
  • Incidentally, $\pi$, like most real numbers, is expected but not known to be normal in base $10$. Because it is expected to be normal, (a) it is possible for some questions, as here, to treat the digits as though they were random, though they are not; and (b) there can't be much of an explanation as to why the $999999$ happens, other than "It just does." ¶ Also, it is not known that Feynman ever remarked about this himself, if I recall rightly. He did, however, make a point similar to the one Ethan Bolker does, in his first-year physics lectures. – Brian Tung May 17 '24 at 21:47
  • It must be indicative of something, besides the redistribution of wealth. – user619894 May 19 '24 at 10:05

4 Answers4

11

The six digit string 141592 is really special. You would expect it to occur eventually, but there it is in $\pi$ right after the decimal point! You can easily calculate the probability of that unlikely early occurrence.

That you find 999999 special is your anthropocentrism. There is no reason to suspect that intelligent life everywhere in the universe counts in base $10$.

In the linked question the explanation for the repeated base $10$ digits is that the number you are expanding is a square root close to the rational number $5000/9$ whose numerator has lots of zeroes and denominator is $10-1$. Mathematicians in other galaxies will find similar repeated digits when they expand similar numbers in their base of choice. You might wonder whether there are bases in which $\pi$ has a similar good approximation.

Ethan Bolker
  • 103,433
  • 1
    The bit about base 10 is straight to the point, but probability theory is not a suitable tool for distinguishing "random" strings from "non-random" ones. (Kolmogorov complexity is.) – Amateur_Algebraist May 17 '24 at 19:35
3

The probability that $5$ next digits of the random sequence will be the same, is $p=10^{-5}.$

The probability that this situation does not take place in $\;N=1000\;$ independent tests, is $$(1-p)^N\approx 1-pN.$$

The probability that we have 5 neighbor digits takes place in N independent tests, is $\;pN\approx 1\%>0.08\%.\;$

Searching for the similar 5-digit subsequences in the decimal digits sequence of $\;\pi\;$ allows to get the table

Table for pi

Similar table can be built for the number $\;e.\;$

Table for e

Obtaining statistic corresponds with $\;p N=10^{-4}\cdot 1000=10\%, \;$ and confirms the model.

Yuri Negometyanov
  • 28,835
  • 1
    You are comparing apples and oranges. The probability of six consecutive 9s in the first 762 digits (say, of a random number between 3 and 4) is about $0.08%$. If we bump it up to the first $1000$ digits, we get about $0.1%$. If we consider repetitions of any other digit as well, we go up to about $1%$. This multiplication by 10 was already mentioned in the question. – Misha Lavrov May 20 '24 at 01:35
0

The sequence 0123456789 happens after17,387,594,880 decimal places but these digits scrambled occur after 60 decimal places. This should be expected if pi is random because ordered digits would be less likely to occur early on. Six nines in succession should have a one in a million chance of randomly occurring However if you give them 700 chances starting from the first decimal places to the 700th then one in a million becomes about one in 1400.And there could have been 9 other digits in a sequence of 6 repeats so we get a probability of around 1400/9 which is about 150. Therefore from the point of view of randomness not really unlikely And we could also look out for sequences like 013579 which are equally probable.

Here is an interesting discussion of patterns in pi https://theconversation.com/pi-might-look-random-but-its-full-of-hidden-patterns-55994

  • The comparison between the ordered and unordered digits is wrong. In a normal number any of the $10!$ permuations of the digits is equally likely to occur first. – Ethan Bolker May 23 '24 at 17:37
-1

Is there a known explanation for the Feynman point?

The cause/effect domain of explaining phenomena does not overlap with the calculation/observation domain of the decimal value of pi. That's why the concept of an "explanation" is inapplicable to this string of digits. The question attempts to unite incompatible fields of knowledge that have different tools, so the answer is neither yes nor no.

Marc Shelikoff
  • 325