0

enter image description here

I have a short section of an ellipse (red) and I wish to find the focal points of that ellipse. I can find the normals at 3 (or more) points on the section.

Given that the normals subdivide the angles between the points and the focal points; can I work backwards to find those focal points?

Update: I can certainly pick 6 points and find their normals and tangents, but my ellipse section will always be (less than) 1 quadrant of the ellipse; and I can't see how to construct the self-crossing hexagon required for Pascal's theorom?

enter image description here

Intelligenti pauca
  • 55,765
Buk
  • 145
  • @user - Doesn't being able to find some normals give some information take the place of knowing some points. – JonathanZ Aug 28 '23 at 18:46
  • @JonathanZ You are correct. I retrieve my close vote. – user Aug 28 '23 at 18:49
  • @user - I think your link to the five-point solution was still useful. Maybe the OP didn't realize that getting a few more points could provide a solution, and it's something that's possible for them? – JonathanZ Aug 28 '23 at 19:01
  • 1
    https://math.stackexchange.com/questions/2070274/graphically-locate-the-axes-or-foci-of-an-ellipse-from-5-arbitrary-points-on-its – user Aug 28 '23 at 19:03
  • @user -- I can obtain 5 or 6 points along with the normals and tangents, but they will always be in the same quadrant of the ellipise, and I cannot see how to construct the self-crossing hexagon for Pascal's theorem? (Am I missing something?) PLeas esee the new image in the OP for clarification of my quandry. – Buk Aug 28 '23 at 20:10
  • See here for Pascal's theorem: https://math.stackexchange.com/questions/3828262/require-a-proof-for-intelligenti-paucas-method-to-compute-an-ellipse/3828379#3828379 – Intelligenti pauca Aug 28 '23 at 20:32
  • But if you can construct the normals at those points, you can also construct the tangents, so you don't need Pascal's theorem. – Intelligenti pauca Aug 28 '23 at 20:33
  • You should also explain if you want an analytic or synthetic solution. In the first figure, it looks like you know the position of the center, is it so? – Intelligenti pauca Aug 28 '23 at 20:55
  • @Intelligenti pauca I have the normals and tangents, but method described in user's link above, requires the generation of a point c' in order to find a diameter, and that is done using pascal's theorem. The drawings above show a section of a known elllipse for analysis and testing. In reality, I will not know the centre. 'scuse my ignorance of math terminology, but I do not know what you mean by "analytic or synthetic solution". – Buk Aug 28 '23 at 21:21
  • I mean: do you have the coordinates of those points and want the equation of the ellipse? Or do you need a compass-and-straightedge construction? – Intelligenti pauca Aug 29 '23 at 07:35
  • Once you have three tangents with their contact point, you can find the center of the ellipse, because the line, passing through the intersection point of two tangents to an ellipse and through the midpoint of their tangency points, also passes through the center of the ellipse. Reflecting one of the points about the center gives another point, in case you need it. – Intelligenti pauca Aug 29 '23 at 07:43

2 Answers2

2

Here's a geometric construction of the ellipse, given three points $P$, $Q$, $R$ on it and two tangents $RT$, $QT$ (see figure below). I won't prove all the details, please ask to know more.

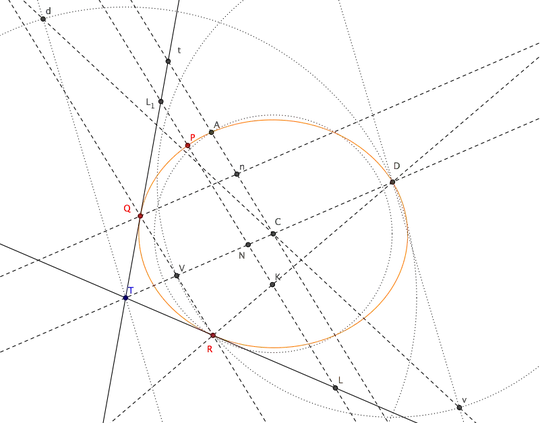
enter image description here

Construct the midpoint $V$ of $QR$: line $TV$ is then a locus of center $C$ of the ellipse. From $P$ construct a line parallel to $QR$, meeting the tangents at $L$ and $L_1$. Construct point $K$ on $LL_1$ such that $LK=\sqrt{LP\cdot L_1P}$; line $RK$ intersects line $VT$ at $D$, which is a point on the ellipse. Center $C$ is that point on $DT$ satisfying: $$ DC:TC=DV:TD $$ (a possible construction of $C$ is shown in the figure: construct $Dv=DV$ parallel to $Td=TD$ and intersect $dv$ with $DT$).

Finally, draw through $C$ a line parallel to $QR$, intersecting tangent $TQ$ at $t$. Let $n$ be the intersection between $Ct$ and the parallel to $TD$ throgh $Q$. Construct $A$ on $Ct$ such that $CA=\sqrt{Cn\cdot Ct}$: point $A$ is then on the ellipse and $CA$, $CD$ are a pair of conjugate semidiameters.

If you want to construct the axes of the ellipse, follow the procedure outlined here.

Intelligenti pauca
  • 55,765
  • Thanks for your time and effort. It turns out that despite that I can manually (trial and error) match an ellipse to my spline very closely -- less than 0.02mm deviatation at any point over the 17.5mm long spline, it can't actually be a section of an ellipse; as when I construct the axes using these methods (I also tried Rytz's construction to obtain them) the resultant ellipse is way off :( I suspect that the first and last points in the spline are bad. I'll try 3 different points, but I'm not confident. Otherwise I'll look for a less formal method of picking my elli – Buk Aug 29 '23 at 18:50
  • @Buk You might try an elliptical fit: https://stackoverflow.com/questions/47873759/how-to-fit-a-2d-ellipse-to-given-points – Intelligenti pauca Aug 29 '23 at 19:41
  • 1
    Success! I tried excluding the first and last knots on the spline, and it was closer. So the I excluded the first two knots each end and the results are very good. I'll post an 'answer' later or tomorrow showing the exact procedure I used -- in case someone comes looking. The spline in question is actually a involute of a circle used in the tooth profile of gears. The fact that it can be accurately approximated using a section of an ellipse is extremely useful. – Buk Aug 29 '23 at 20:41
  • This is the most complicated solution I read today. – Bob Dobbs Aug 29 '23 at 22:35
  • @Bob Dobbs -- You have a simpler solution? – Buk Aug 30 '23 at 00:42
1

enter image description here

The gif shows the process I used to derive an ellipse to closely approximate my spline, which is actually the involute of a circle profile of the meshing surface of a gear tooth.

  1. The first frame shows the source of the spline.
  2. The second the spline in isolation.
  3. 3 - 5 the chosing of 3 points, inset from the ends and roughly the middle.
  4. 6 - 8 the construction of 3 tangents at those points.
  5. 9 & 10 the chords between them.
  6. 11 & 12 projecting the centre of the ellipse.
  7. 13 projecting one of the conjugate diameters.
  8. 14 projecting the second conjugate diameter, calculated according to the first pair of formulae from Intelligenti pauca here.
  9. 15 - 19 Finding the axis using Rytz's construction

10 20 - 22 drawing the ellipse and inspecting the fit.

Buk
  • 145
  • OK, this should give the same solution as in my amswer, the only difference being that I avoided using a third tangent to give a more general construction, while you used it to find the center. – Intelligenti pauca Aug 30 '23 at 08:23
  • And of course you could use the spline to find other points on the ellipse as intersections, which probably helped to give a better approximation. – Intelligenti pauca Aug 30 '23 at 08:31
  • 1
    @Intelligenti pauca -- What I found with that method is that as the angle between my two tangents and the chord is so shallow, the L-L1 line becomes very long, thus exacerbating any discrepancies. Using the 3 tangent method you described elsewhere seems to extract more data from the spline itself, and kept the construction more compact. – Buk Aug 30 '23 at 12:00
  • @Intelligenti pauca -- I tried the ultimate extension of interpolating additional points on the ellipse, by reflecting the spline about both axes: https://i.imgur.com/6uyKndu.png; but as the information used to construct the axes is already derived, it does seem to add more data? Ditto, once the centre has been located using points generated using that centre do not seem to add accuracy. (Maybe I did it wrong?) – Buk Aug 30 '23 at 12:04
  • The problem is your spline is not really an arc of ellipse, hence the result depends on which points you choose. In this case the best result should be obtained from a least-square fit. But if you must do this just once, your hand-fitted method is fine. – Intelligenti pauca Aug 30 '23 at 12:12
  • @Intelligenti pauca -- I'm hoping to define the diameter and section angle of generating cylinders for a range of gear sizes. A 20T m1 gears teeth are simply a 0.1 scaling of a 20T m10 gear, so the same ellipse can be scaled for any gear with the same number of teeth. The involute is generated by rolling a straight side rack around a base circle (see http://www.me-bac.com/temp/img2_gmf5o5uu1qnjrjrjevn87fs9q5.svg?1693404147569) and any number of points can be generated. Having proven it can be done, I'll write code to do the others. – Buk Aug 30 '23 at 14:30
  • Let us continue this discussion in chat. – Buk Aug 30 '23 at 15:30