4

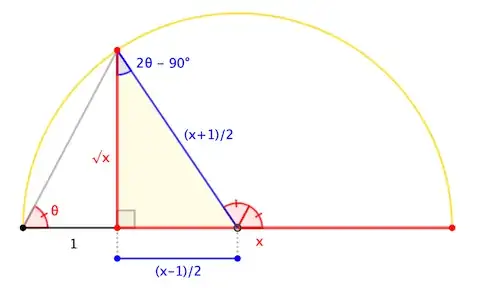
So I started by saying that $$y=\arcsin\left(\frac{x-1}{x+1}\right)$$

Then you could say that $$\sin(y)=\frac{x-1}{x+1}$$

Then calculating $\cos(y)$ with the trigonometric identity, I found the following:

$$\cos(y)=\frac{x-1}{2\sqrt{x}}$$

If I then calculate $\tan(y)$ and take the inverse of that I hoped to find the right hand side, but instead I found

$$\arctan\left(\frac{x-1}{2\sqrt{x}}\right)$$

Now I used wolfram to check if they are equal and it gives a solution so I'm guessing an intersection at $x=1$. There also is an extra question that asks for what real value of $x$ this expression makes sense.

lynx_s
  • 87
  • I might have found something, but I'm not sure if it's correct to do/say that, If the derivatives are equal does that mean the functions are equal? Because their derivatives are equal – lynx_s Aug 16 '23 at 14:14
  • You can also see that it is equal to derivative of $2\arctan{(\sqrt x)}+1$ it will also be equal to other derivatives, so no it doesn't mean that functions are equal if their derivatives are equal. – bb_823 Aug 16 '23 at 14:17
  • Both sides lie in the range $[-\pi/2,\pi/2]$, so taking $\sin$ of both sides can't introduce extraneous solutions. Then use trig identities. – eyeballfrog Aug 16 '23 at 14:30

5 Answers5

5

you can write

$$ y = \arctan(\frac{x-1}{2\sqrt{x}}) $$

as

$$ y = \arctan(\frac{\sqrt{x}-\frac{1}{\sqrt{x}}}{2}) $$

then you use the identity

$$ \arctan x - \arctan y = \arctan(\frac{x - y}{1 + xy}) $$

you can re-write y as

$$ y = \arctan(\sqrt{x}) - \arctan(\frac{1}{\sqrt{x}}) $$

$$ y = \arctan(\sqrt{x}) - \frac{\pi}{2} + \arctan(\sqrt{x}) $$

which is what you need

Vanessa
  • 489
3

Here's a trigonographic demonstration for $x\geq 1$.

enter image description here

$$\tan\theta = \sqrt{x} \quad\to\quad \sin(2\theta-90^\circ) = \frac{x-1}{x+1}$$

Adapting it for $0\leq x<1$ is left as an exercise to the reader.

Blue
  • 83,939
1

You found that $\sin(y)=\frac{x-1}{x+1}$. After that you can take $\sin$ of left side. You get $$\sin(2\arctan{\sqrt x}-\frac{\pi}2)=\sin{(2\arctan{\sqrt x})}\cos{\frac{\pi}2}-\cos{(2\arctan{\sqrt x})}\sin{\frac{\pi}2}=\\-\cos{(2\arctan{\sqrt x})}=\sin^2{\arctan{\sqrt x}}-\cos^2{\arctan{\sqrt x}}=\frac{x}{1+x}-\frac{1}{1+x}=\frac{x-1}{x+1}$$

From ther we have $\sin y=\sin(2\arctan{\sqrt x}-\frac{\pi}2)$ and since the codomain of both functions is $[\frac{-\pi}{2},\frac{\pi}{2}]$ we can say $\arcsin{\frac{x-1}{x+1}}=2\arctan{\sqrt x}-\frac{\pi}2$.

bb_823
  • 2,709
1

Another way to prove that

$\arcsin\left(\dfrac{x-1}{x+1}\right)=2\arctan\left(\sqrt{x}\right)-\dfrac{\pi}2\;\;\;$ for any $\,x\geqslant0\,.$

Proof :

For any $\,x\geqslant0\,,\;$ let $\,\alpha_x\in\left[0,\dfrac{\pi}2\right)\,$ such that $\,\sin\alpha_x=\sqrt{\dfrac x{x+1}}\;.$

It results that $\;\cos\alpha_x=\sqrt{\dfrac1{x+1}}\;,\;\,$ $\tan\alpha_x=\sqrt x\;.$

Moreover ,

$\begin{align}\arcsin\left(\dfrac{x-1}{x+1}\right)&=-\arcsin\left(\dfrac{1-x}{x+1}\right)=-\arcsin\left(\cos^2\!\alpha_x-\sin^2\!\alpha_x\right)=\\[3pt]&=-\arcsin\!\big(\!\cos\left(2\alpha_x\right)\big)=-\arcsin\!\left[\sin\left(\dfrac{\pi}2\!-\!2\alpha_x\right)\right]=\\[3pt]&=-\left(\dfrac{\pi}2\!-\!2\alpha_x\right)=2\alpha_x-\dfrac{\pi}2=2\arctan\!\big(\!\tan\alpha_x\big)-\dfrac{\pi}2=\\[3pt]&=2\arctan\left(\sqrt x\right)-\dfrac{\pi}2\;.\end{align}$

Angelo
  • 13,952
1

WLOG, $\arctan\sqrt x=y$

As for real $x,\sqrt x\ge0$

$\implies0<y<\dfrac\pi2$

So, the RHS becomes $?$

The LHS $=\arcsin\dfrac{x-1}{x+1}=\arcsin(-\cos2y)=-\arccos(\cos2y)+\dfrac\pi2$

Finally for $0<2y<\pi, \arccos(\cos2y)=+2y$

lab bhattacharjee
  • 279,016