Conceptually Understanding the Mathematical Definition for an Envelope of Family of Curves

Question

Assuming we have a one-parameter, two-dimensional, family of curves, given by $f(x, y, p) = 0$, there are two requirements for the envelope (see https://en.wikipedia.org/wiki/Envelope_(mathematics)#) of that family (assuming it exists):

$$\begin{Bmatrix} &f(x, y, p) &= &0& \\ &\frac{\partial}{\partial p} \left[f(x, y, p)\right]&= &0&\end{Bmatrix}$$

Now, this first requirement makes sense, as the envelope curve must itself sit on a point from the family of curves.
But I'm having trouble conceptually wrapping my mind around this second requirement and what it means.

Answer 1

Most text books which over this Concept generally hand-wave or gloss-over the mathematics behind the Equations.

Yes , I agree with OP that it is not very clear why $ \frac{\partial f(x,y,p)} {\partial p} $ must be $0$.

Eg , the given wiki brushes-off the Issue by claiming $f(x,y,p_1)=0$ & $f(x,y,p_2)=0$ , hence $f(x,y,p_1)-f(x,y,p_2)=0$ & almost "magically" , it concludes that $\frac{f(x,y,p_1)-f(x,y,p_2)}{(p_1-p_2)}=0$ , which is not intuitive : (1) Why not divide by $(p_1-p_2)^2$ ? (2) Why not say the Same for Elementary Differential Calculus to claim that $dy/dx=0$ always ? (3) Why not consider $\frac{\partial f} {\partial x} = 0$ with Same logic ? (4) Why 2 Criteria are enough ?
In short , the given Derivation is incomplete or inaccurate.

It is similar in most other text books too.

I will try to give my intuition & then I will give the Correct Derivation.
Best (Complete) Derivation I came across was in Myskis (Mir Publishers) "Introductory Mathematics for Engineers" & my Elaboration (Calculation) will be utilizing that.
It may look a little too long but it is essential very simple.

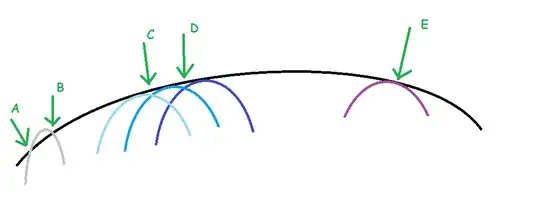
Consider the Black Envelope & the Grey Isolated Curve & the family of Curves which have that Envelope.

When the left-most Grey curve is intersecting on the left (Point $A$) , the tangents (to the curve & to the Envelope) are Positive but not equal.
At the Intersection on the right (Point $B$) , one tangent is going up while the other is going down.
Naturally , we can see that the Grey Curve can not have the Envelope shown at that Point.
Let us ignore the Grey Curve , which is not in the family of curves & is shown to high-light what the tangents must be like.

Consider the right-most Purple curve.
The tangent to Envelope & the tangent to Curve are coinciding , having Exact Same value at $E$ , the Point of Contact.
This is what we want from 2 Consecutive Curves.

Consider the Central Blue Curve corresponding to some $p$.
To the left , we have the Curve corresponding to $p - \delta p$.
To the right , we have the Curve corresponding to $p + \delta p$.

The Points of Intersection are $C$ & $D$ which lie on the Curves hence $f(x,y,p)=0$.
$C$ : Intersection of $f(x,y,p - \delta p)=0$ & $f(x,y,p)=0$
$D$ : Intersection of $f(x,y,p)=0$ & $f(x,y,p + \delta p)=0$
We can not make $\delta p \equiv 0$ , because all Points between 2 Curves will be Common.
When $\delta p$ tends to $0$ , the Points $C$ & $D$ get closer to the Envelope & will eventually lie on the Envelope.
Here , hand-waving intuition : $f(x,y,p + \delta p) - f(x,y,p) \equiv 0$ , $\frac{f(x,y,p + \delta p) - f(x,y,p)}{\delta p} \equiv 0$ , hence we can "eliminate" $\delta p$ by taking limit when it tends to $0$

Derivation (utilizing material given by Myskis) :

We have $f(x,y,p) = 0$ on the Curves & on the Envelope.
Let $p=C$ , some value , corresponding to a Point on the Envelope , hence $f(x,y,C) = 0$.

Let $y_{envel}(x)$ be the Envelope , while $y_{curv}(x)$ be the Curve at the Point we are focussing on here.

When we move along the Envelope (varying the $x$ co-ordinate) , naturally $C$ will change , that is , $C=C(x)$
Partially Differentiate the given function to get :
$\color{blue}{\frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} \frac{dy_{envel}}{dx}} + \color{green}{\frac{\partial f}{\partial C} \frac{dC(x)}{dx}} = 0 \tag{1}$
When we move along the Curve (varying the $x$ co-ordinate) , we keep $C$ Constant , that is , $\frac{dC}{dx}=0 \tag{2}$
Partially Differentiate the given function to get :
$\color{blue}{\frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} \frac{dy_{curv}}{dx}} + \color{red}{\frac{\partial f}{\partial C} \frac{dC}{dx}} = 0 \tag{3}$

At the Point of Contact between Curve $y_{curv}(x)$ & Envelope $y_{envel}(x)$ , we want the two tangents to be Equal , that is , $\frac{dy_{curv}}{dx}=\frac{dy_{envel}}{dx} \tag{4}$ , which will Equalize the 2 blue Parts in (1) & (3)

In (3) , the red Part is $0$ , hence the remaining blue Part is $0$.
We can plug that into (1) to make the green Part $0$.

In general , We know $C(x)$ is not a Constant in green Part , hence we are left with $ \frac {\partial f} {\partial C} = 0 $

Thus we got what we wanted : $\frac {\partial f} {\partial p} = 0 $

Most text books avoid the Elaborate Details & simply hand-wave to give the Criteria. The exception is Myskis who has given the Details.

Answer 2

I won't be adding anything else to the previous answers but a piece of imagination and loose interpretations to bring a physical intuition about.

A moving point running along the envelope

If you look carefully the animation of an sliding bar on the envelope page of the wikipedia, you'll agree with me, we can think of the envelope as a rail $\Gamma(x)$ guiding a moving point.

Lets such point $x$ be parameterized by $t$ $|$ $x=x(t)$ and $\Gamma(x(t))$.

The derivative,

$$ \Gamma'(x(t)) = \frac{\partial\Gamma}{\partial x} \cdot \frac{\partial x}{\partial t} $$

The mobile point actually exists within a family of curves $ y = C(x,t)$ so the differential of its movement is,

$$ dC(x,t) = \frac{\partial C}{\partial x} dx + \frac{\partial C}{\partial t} dt $$

Diving by $dt$,

$$ \frac{dC(x,t)}{dt} = \frac{\partial C}{\partial x} \frac{dx}{dt} + \frac{\partial C}{\partial t} \frac{dt}{dt} $$

Or simply,

$$ \frac{dC(x,t)}{dt} = \frac{\partial C}{\partial x} \frac{dx}{dt} + \frac{\partial C}{\partial t} $$

Since $C$ and $\Gamma$ are coincident for the moving point, $ y = C = \Gamma $, at that particular point,

$$ \frac{\partial\Gamma}{\partial x} \cdot \frac{\partial x}{\partial t} = \frac{\partial C}{\partial x} \frac{dx}{dt} + \frac{\partial C}{\partial t} $$

So, $ \frac{\partial C}{\partial t} $ has to equal 0 at that point.

The first meaning I can think of for the derivative condition equaling $0$ is:

Meaning 1

The approximation point behaves like a composed movement.

Base & Roulette on an elastic band

Observing the same animation on the wikipedia we can also deduce that the family of curves kind of rotate around the approximation (contact) point. We cannot speak about a rigid solid but its similar to a stationary node in the solution of a partial differential equation.

When looking at the differential of a family of curves,

$$ dC(x,t) = \frac{\partial C}{\partial x} dx + \frac{\partial C}{\partial t} dt $$

we can interpret it as a movement in the same curve (the $dx$ part), and a movement due to the shape shifting (the $dy$ part).

A point would be "stationary" if it shares it's tangent vector with the adjacent curve in the family. To put it another terms, there is point movement ($\frac{\partial y}{\partial x}$) but not surface shaking ($\frac{\partial y}{\partial t}$)

So the derivative condition implies some extra meanings,

Meaning 2

The envelope is the locus of the "stationary node" of a family of curves.

Meaning 3

The envelope is the locus of all the common adjacent tangents of a family of curves.

Notice that two curves sharing a tangent vector don't slide one upon the other.

Meaning 4

The envelope is the surface that the curve family rolls upon without sliding.

A beautiful video

PhysicsGrad made this beautiful video showing the curve family in 3D and gives a mathematical explanation of why the derivative has to be 0 using Rolle's theorem.

https://youtu.be/akF6NoIErus?si=zFpwFxTsEEE5BdSS

I hope it helps you on grasping an intuitive sense on what is going around this subject.