7

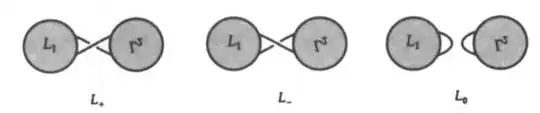
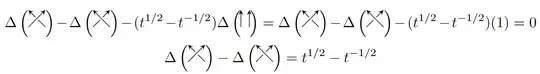For (one of) the books I am using to learn knot theory, the Alexander polynomial is defined by the skein relation, or the unknot has polynomial 1 and the relation $\Delta(L_+)-\Delta(L_-)+(t^{1/2}-t^{-1/2})\Delta(L_0) = 0$. Following this, the book (The Knot Book by Colin Adams) says that it works under the Reidemeister moves.

However, from this definition I am struggling to prove it. Consider a Type I one move being applied on the unknot. I have attached an image of what I think should be the case, but I can't seem to work it out since $L_+$ and $L_-$ don't cancel. Could someone possibly provide guidance? I feel like I'm approaching it wrong, but I don't know how, and searching around online it seems generally to be skipped over. Thank you!

enter image description here

Edit: I think it is possible this is missing an axiom? Some of the other definitions I have found have the polynomials being equivalent under ambient isotopy being an axiom. Is that what's going wrong?

junglekarmapizza
  • 171
  • @MarianoSuárez-Álvarez Okay, that makes more sense. The way the book presents it is more as a definition rather than a list of conditions, which is part of why I was confused. I had learned bracket and Jones polynomial before and with those you prove the explicitly the Reidemeister moves work, so I think that was adding to the confusion as well. Thanks for the help! – junglekarmapizza Aug 07 '23 at 04:26
  • @junglekarmapizza Part of the reason for the discrepancy is that the Jones Polynomial is best defined combinatorially to start (there is a TQFT definition, but it's a bit abstract to prove anything with) while the Alexander Polynomial is usually defined in terms of the homology of a cover of the knot complement (which makes it immediately obvious that it's a knot invariant, and is actually calculatable in terms of Seifert matrices). It's more standard to define it that way then derive the Skein relation. That said, you might look at proofs for the HOMFLY polynomial. – Brevan Ellefsen Aug 07 '23 at 17:55

1 Answers1

4

If your question is whether ambient isotopy is allowed, then: yes, it is by definition.

However, we must show this is well-defined with regards to the other axiom. Thus, assuming I understand you correctly, you wish to show the Skein relation is well-defined under a Reidemeister move, in particular a Type I move. We use the convention $\nabla(O) = 1$ and $\nabla(L_+)-\nabla(L_+) = z\nabla(L_0)$.

The first thing to prove is that $\nabla(O \sqcup L) = 0$ for any link $L$. Indeed, this is true more generally: any splittable link (meaning one of the components can be separated from the others by a plane after an ambient isotopy) has Alexander polynomial $0$. To prove this, consider the following diagram 6.35 from Adams' book:

enter image description here

Specifically, we think of the third diagram $L_0$ as our splittable link , with the left circle being the splittable component and the right circle being the remaining components. We could imagine joining the two components together as shown in the first two diagrams $L_+$ and $L_-$, but both of these are just the connected sum! (imagine flipping the right circle in the first diagram down, and flipping the same circle in the second diagram up). As such, $\nabla(L_-) = \nabla(L_+)$ so that, by the Skein relation, $z \nabla(L_0) = 0$ from which we conclude $ \nabla(L_0) = 0$.

The proof of invariance under the first Reidemeister move (of either type) then follows directly: if we first orient the link $L$ and then apply the Skein relation to a Type I move, we find both $L_+$ and $L_-$ are ambient isotopic to the original link $L$ so have the same Alexander polynomial. Moreover, $L_0 = O \sqcup L$ so that $\nabla(L_0) = 0$ by the above lemma. We thus have $\nabla(L_+)-\nabla(L_+) = z\nabla(L_0) = 0$ as claimed.

Brevan Ellefsen
  • 15,317