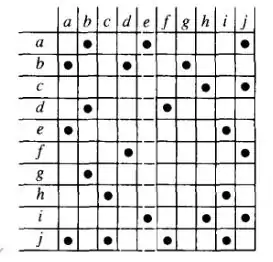
In the adjoining table, a dot indicates the combination of chemicals that cannot be placed in the same location as the other because of safety issues. If a company is dealing with the chemicals a,b,c,d,e,f,g,h,i,j listed in the table, what is the minimum number of storage locations needed by the company?
My idea of the solution is something like this:
I start with 'a'. I can collocate it with c,d,f,g,h,i, but not with b,e,j. But then, I note that d and f cannot be collocated. How/where do I go from here?