How to mathematically model my population growth simulation

Question

In high-school we learn to model population growth as an exponential, but we know that this is different from reality because population growth seems to hit as asymptote as some point due to limited resources. I wanted to see if I could recreate this effect with a computational model.

The model I came up with was based around the concept of what I'm calling a cell. A cell keeps track of its age, how many resources it has (which for the purpose of my model is a single number and is limited to 10000 for the entire population), and whether or not it is alive. The simulation starts with a single cell that has 2 resources. Each iteration of the simulation it loses a resource. It also has a 70% chance of gaining a resource, and 30% chance of gaining 2 additional resources, and a ten percent chance of gaining 3 additional resources, potentially gaining up to 6 resources in one iteration. If the cell has greater than 4 resources, it has a 50% chance of creating a new cell. The new cell starts with 2 resources, taken from its parent cell. Each cell also has an age-related chance of dying, dying for certain on its 10th iteration.

When I ran this simulation I was able to get a nice asymptote at around 38,000, so it was cool to see the asymptotic behavior come out of the model.

I started thinking how I would go about mathematically modeling this, though. Based on the parameters that I've picked, I would think there should be an analytic way to come up with numbers like the average maximum number of cells the resources could sustain. How would I go about thinking through a problem like that, perhaps coming up with a differential equation to model this kind of behavior.

I was able to find the logistic equation for population growth:

$$\frac{dP}{dt} = rP \left( 1 - \frac{P}{K} \right)$$

where $P(t)$ is the population at time t, r is the relative growth rate, and $K$ is the carrying capacity of the population. This seemed like a sensible model, but a few questions:

1. How would you come up with something like that based on knowing just the rules of the simulation? It seems reasonable, but not also totally obvious.
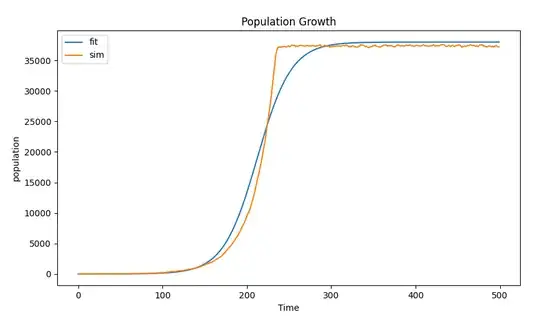
2. Why does it not fit my data during the population growth phase (see the image below). The steepness of my slope always seems greater than the fit to the logistic equation.

I attempted to fit the solution to the differential equation using scipy:

$$P(t) = \frac{K}{1+Ae^{-rt}}$$

where

$$A = \frac{K-P_0}{P_0}$$

where $P_0$ is the initial population (1 in my case). The image of the fit during the growth and the code used to do the simulation and create the plot is provided below. If you choose to run the code, you'll likely have to attempt it several times for the population growth to actually take off. You can probably lower the number of iterations, all of the growth seems to happen in the first 250 iterations or so, but the way I actually ran it is below.

import numpy as np
from random import random
import scipy
import matplotlib.pyplot as plt
import math
iterations = 10000
population = np.array([-1]*iterations)
resources = 100000
members = []
rate_of_one_success = 0.7
rate_of_two_success = 0.3
rate_of_three_success = 0.1
rate_of_reproduction = 0.5
rate_of_death = [0.1, 0.1, 0.1, 0.1, 0.1, 0.2, 0.2, 0.3, 0.3, 1]
class Cell:
    def init(self, gen, resources):
        self.generation = gen
        self.age = 0
        self.resources = resources
        self.alive = True
time = 0
members.append(Cell(1, 2))
while time < iterations:
    print(time)
    new_members = []
    population[time] = len(members)
    for mem in members:
        mem.resources = mem.resources - 1
        resources = resources + 1
        if resources > 0 and random() < rate_of_one_success:
            resources = resources - 1
            mem.resources = mem.resources + 1
        if resources > 1 and random() < rate_of_two_success:
            resources = resources - 2
            mem.resources = mem.resources + 2
        if resources > 2 and random() < rate_of_three_success:
            resources = resources - 3
            mem.resources = mem.resources + 3
        if random() < rate_of_reproduction and mem.resources >=4:
            new_members.append(Cell(mem.generation+1, 2))
            mem.resources = mem.resources - 2
        if mem.resources < 1:
            mem.alive = False
            resources = resources + mem.resources
        if random() < rate_of_death[mem.age]:
            mem.alive = False
            resources = resources + mem.resources
        mem.age = mem.age + 1
    members = [mem for mem in members if mem.alive]
    members = members+new_members
    time = time + 1
    print(resources)
def log_eqn(t, K, r):
    return K/(1+(K-1)np.exp(-rt))
t=list(range(0,len(population)))
fit = scipy.optimize.curve_fit(log_eqn, list(t[0:500]), list(population[0:500]))
K = fit[0][0]
r=fit[0][1]
print("K={}".format(K))
print("r={}".format(r))
plt.figure(figsize=(5, 2.7))
plt.plot(t[0:500], [K/(1+(K-1)math.exp(-rx)) for x in t[0:500]], label="fit")
plt.plot(t[0:500], population[0:500], label="sim")
plt.xlabel("Time")
plt.ylabel("population")
plt.title("Population Growth")
plt.legend()
plt.show()
````

Answer 1

The answer requiers data on numerical form. Unfortunately only a graph is joint to the question.

As a consequence the data used below are not the original data but were imported from a scanning of the available graph. This is not accurate especially for the low values of (x,y).

The approximate experimental points are represented on x-linear and y-linear scales (at left) as well as on x-linear and y-logarithmic scales (at right) :

In the area mentioned as "bad data import" the points are not well defined due to the low definition of the scanned pixels. So the above study and results will have no signifiance in this range. This is a pity to not work with correct data : It will be impossible to adjust a model well convenient in the range of low (x,y) wich is important at the origin of the population.

On the lin-log graph one observe a well defined straight line on the medium range. Thus the function is close to exponential.

The exponential growth is limited by a well defined plateau.

From this inspection one can define a model equation (blue curve) made of an exponential function and a linear function (horizontal line) both linked thank to the Heaviside function :

The fitted function (blue line) and the data points (red) are quite indistinguishable one from the other except in the area of "bad data import".

ANOTHER EQUATION MODEL

Continuing the inspection one observe on the x-linear and y-logarithmic graph that the derivative of $\log(y)$ is roughly a step function (positive for $x<235$) and ($\simeq 0$ for $x>235$). This shape can be approximated with a function of logistic kind :

$$\frac{d}{dx}\ln(y)\simeq \frac{b}{1+e^{\,p\,(x-c)}}$$

Integrating leads to

$$y\simeq a\:\frac{e^{\,b\,(x-c)}}{\left(1+e^{\,p\,(x-c)}\right)^{b/p}}$$

Data points in red. Fitted function in blue.

The transition between the exponential growth and the plateau is better with this model than with the preceeding.

As already pointed out the model is not accurate for the low values of $y$. Adding a constant $C$ slightly improves the fitting around the origin as shown below. But probably this isn't the best way. With more correct data one could try to modify the model equation in order to improve the fitting in this area.