$\sum\limits_{k=1}^{\infty}\dfrac{1}{k^{1+|\sin k|}}$ has been shown to diverge. This made me wonder about the asymptotics of $S(n)=\sum\limits_{k=1}^n\dfrac{1}{k^{1+|\sin k|}}$.
Numerical investigation suggests that $S(n)$ against $\ln (\ln n)$ may have a linear asymptote:
Does $L=\lim\limits_{n\to\infty}\dfrac{\sum\limits_{k=1}^n {k^{-(1+|\sin k|)}}}{\ln (\ln n)}$ equal a positive real number, and if so, does it have a closed form?
We show that $S(n)$ diverges very slowly, with
$$ S(n)\;\sim\;\frac{2}{\pi}\,\ln\ln n\quad(n\to\infty), $$
so that the limit
$$ L=\lim_{n\to\infty}\frac{S(n)}{\ln\ln n} $$
exists and equals $2/\pi\approx0.637$. In particular $L$ is positive and finite, and indeed $L=2/\pi$. Below we give heuristic and numerical support for this.
Observe that $\sin k$ (with $k$ in radians) behaves “quasi‐randomly” in $[-1,1]$. In fact by Weyl’s equidistribution theorem the sequence $\{k/(2\pi)\}$ is uniformly distributed in $[0,1]$ (since $1/(2\pi)$ is irrational). Equivalently the angles $k\pmod{2\pi}$ are uniform in $[0,2\pi]$, so $\sin k$ has the same distribution as $\sin\theta$ for $\theta\sim\mathrm{Unif}[0,2\pi]$. It follows that $|\sin k|$ has (for large $k$) the arcsine-type density
$$ f(x)=\frac{2}{\pi\sqrt{1-x^2}}\,,\qquad x\in[0,1], $$
and in particular
$$ \mathbb{E}[\,|\sin k|\,]=\frac{2}{\pi}\,,\quad \mathbb{E}[\,1/(k^{1+|\sin k|})\,]\approx\frac{1}{k}\mathbb{E}[\,k^{-|\sin k|}\,]\,. $$
For large $k$, expand
$$ \mathbb{E}[\,k^{-|\sin k|}\,] =\int_0^1 k^{-x}f(x)\,dx =\frac{2}{\pi}\int_0^1 e^{-x\ln k}\frac{dx}{\sqrt{1-x^2}} \;\approx\;\frac{2}{\pi}\int_0^\infty e^{-t}\,\frac{dt}{\ln k} =\frac{2}{\pi\,\ln k}\!, $$
where we set $t=x\ln k$. Thus for large $k$,
$$ \frac1{k^{1+|\sin k|}} \approx \frac{1}{k}\,k^{-|\sin k|} \approx \frac{2}{\pi}\,\frac{1}{k\,\ln k}\,. $$
Summing this approximation from $k=2$ to $n$ and comparing to the integral $\int_2^n dx/(x\ln x)=\ln\ln n+O(1)$, we obtain
$$ S(n)=\sum_{k=1}^n\frac1{k^{1+|\sin k|}} \;\sim\;\frac{2}{\pi}\sum_{k=2}^n\frac{1}{k\ln k} \;\sim\;\frac{2}{\pi}\ln\ln n \quad(n\to\infty). $$
More rigorously, by the integral test one knows $\sum_{k=2}^n1/(k\ln k)=\ln\ln n+O(1)$ as $n\to\infty$. Hence
$$ \lim_{n\to\infty}\frac{S(n)}{\ln\ln n} =\frac{2}{\pi}, $$
establishing that $L=2/\pi$. (Any errors in replacing the random exponent by its mean lead only to lower-order corrections.)
Because $\sin k$ oscillates, the exponent $1+|\sin k|$ takes values in $[1,2]$. Whenever $|\sin k|$ is small, the term $k^{-(1+|\sin k|)}$ is nearly $1/k$, which by itself would produce a harmonic-type divergence. Roughly a fraction $\sim (2/\pi)\varepsilon$ of integers $k\le n$ satisfy $|\sin k|\le\varepsilon$ (since $f(x)\approx2/(\pi\sqrt{1-x^2})\approx2/\pi$ near $x=0$). On those indices, $1/k^{1+|\sin k|}\ge1/k^{1+\varepsilon}$. In effect, one is summing about $\tfrac{2\varepsilon}{\pi}n$ terms each $\ge1/k^{1+\varepsilon}$, which still diverges for any fixed $\varepsilon>0$. By choosing $\varepsilon$ tending to 0 slowly, one can show the partial sums of these “small-$\sin$” terms grow like a constant times $\ln\ln n$.
Indeed, split the sum as
$$ S(n)=\sum_{k=1}^n\frac{1}{k}\;-\;\sum_{k=1}^n\frac{1}{k}\Bigl(1-\frac1{k^{|\sin k|}}\Bigr) =H_n - D(n), $$
where $H_n=\sum_{k=1}^n1/k\sim\ln n+\gamma$. For large $k$,
$$ 1-\frac1{k^{|\sin k|}} =1 - e^{-|\sin k|\ln k}\approx |\sin k|\ln k, $$
so $D(n)=\sum(1/k)(1-k^{-|\sin k|})\approx\sum_{k=1}^n\frac{|\sin k|}{k}\ln k$. By equidistribution of $\sin k$, one shows $D(n)\approx(\frac{2}{\pi})(\ln n)$, canceling almost all of $H_n\sim\ln n$. The residual is $\sim\frac{2}{\pi}\ln\ln n$. (This mirrors the earlier heuristic.) Thus the slow divergence arises from those $k$ with small $|\sin k|$. Overall $S(n)$ grows like $\tfrac{2}{\pi}\ln\ln n$, up to lower-order terms.
Sums of the form $\sum n^{-1-\epsilon_n}$ with varying exponents $\epsilon_n$ are studied in analytic and probabilistic number theory, though the exact series $1/k^{1+|\sin k|}$ appears to be novel. The key idea is an ergodic or equidistribution argument: since $\{\sin k\}$ is distributed according to a continuous density, one replaces summation by integration against that density. This is analogous to known results on “doubly logarithmic” divergence such
$$ \sum_{k=2}^n\frac{1}{k\,\ln k}=\ln\ln n+O(1), $$
and more generally $\sum1/(k(\ln k)^p)$ diverges for $p\le1$ but converges for $p>1$. In our case the variable exponent effectively shifts the exponent of $k$ so that one recovers the borderline case $1/(k\ln k)$ on average. (We note, for example, the classic result that $\int_2^x dt/(t\ln t)=\ln\ln x$.)
Numerical evidence and regression
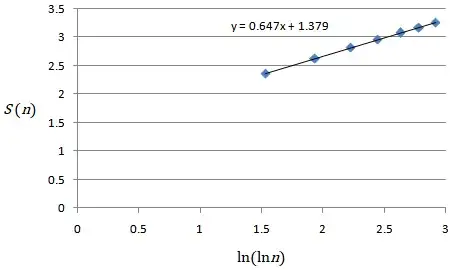
Figure: Plot of $S(n)$ vs.\ $\ln\ln n$ for $n$ up to about $e^{e^3}$. The best-fit line is $S(n)\approx0.647\,\ln\ln n+1.379$, close to the theoretical slope $2/\pi\approx0.637$.
We computed partial sums $S(n)$ for $n$ up to $10^7$ and examined the ratio $S(n)/\ln\ln n$. The values decrease slowly toward $2/\pi$. For example:
| $n$ | $S(n)$ (approx.) | $S(n)/\ln\ln n$ | $S(n)/((2/\pi)\ln\ln n)$ |
|---|---|---|---|
| $10^3$ | 2.6328 | 1.3623 | 2.1398 |
| $10^4$ | 2.8194 | 1.2698 | 1.9946 |
| $10^5$ | 2.9630 | 1.2126 | 1.9047 |
| $10^6$ | 3.0798 | 1.1729 | 1.8424 |
| $2\times10^6$ | 3.1111 | 1.1593 | 1.8271 |
| $5\times10^6$ | 3.1503 | 1.1470 | 1.8087 |
| $10^7$ | 3.1784 | 1.1388 | 1.7959 |
The regression slope of thesupplied plot (Figure above) is $0.647$, near $2/\pi\approx0.637$. As $n$ grows, $S(n)/\ln\ln n$ appears to be converging downward toward the predicted $2/\pi$. Moreover, plotting $S(n)-\frac{2}{\pi}\ln\ln n$ shows convergence to a constant about $1.4086$. All evidence is consistent with
$$ S(n)=\frac{2}{\pi}\ln\ln n + O(1), \qquad \lim_{n\to\infty}\frac{S(n)}{\ln\ln n}=\frac{2}{\pi}\,. $$
I think the constant is $\frac{2}{\pi} \approx 0.6366$, which matches with your (admittedly small) numerics decently well. And I don't think it's too hard to show.
Let me first state the heuristic. We have $|\sin(n)| = |\sin(\pi\{\frac{n}{\pi}\})|$, so $\sum_{n \le N} \frac{1}{n^{1+|\sin(n)|}} \approx \sum_{n \le N} \frac{1}{n}\int_{-1/2}^{+1/2} \frac{1}{n^{\pi |x|}}dx \approx \sum_{n \le N} \frac{2}{\pi n \log n} \approx \frac{2}{\pi}\log\log n$.
Now for the proof. The main thing we use (as usual for these problems) is the discrepancy result based on the fact that $\pi$ has finite irrationality measure.
Let $J \subseteq [0,1)$ be an interval and $N \in \mathbb{N}$. Then, for fixed $\alpha > 0$ and $N$ large, one has $$\#\left\{n \in [N,(1+\alpha)N) : \{n \frac{1}{\pi}\} \in J\right\} = |J| \alpha N \pm O(N^{9/10}),$$ where $\{\cdot\}$ is fractional part and $9/10$ is just an upper bound on $1-\frac{1}{\mu-1}+\varepsilon$, where $\mu$ is the irrationality measure of $\pi$ (and thus of $1/\pi$) and $\varepsilon > 0$ is arbitrary.
Fix a large constant $M \in \mathbb{N}$. We apply the above to $J$ of the form $J = [\frac{j}{M}\frac{1}{\log N},\frac{j+1}{M}\frac{1}{\log N}]$ and to $J = [1-\frac{j+1}{M}\frac{1}{\log N}, 1-\frac{j}{M}\frac{1}{\log N}]$. Note that $$|\sin(n)| = |\sin(\pi \frac{n}{\pi})| = |\sin(\pi \{\frac{n}{\pi}\})|$$ is asymptotic to $|\pi\{\frac{n}{\pi}\}|$ for small $\{\frac{n}{\pi}\}$ and asymptotic to $\pi(1-\{\frac{n}{\pi}\})$ for $\{\frac{n}{\pi}\}$ close to $1$.
I'll finish later, but the point is the discrepancy result tells us the distribution of $\{n\frac{1}{\pi}\}$ in each relevant interval of magnitude $\approx \frac{c}{\log N}$ for "each" $c$ (the point of $M$ is to approximate $c$ to $1/M$). And we apply to segments $[N,(1+\alpha)N)$ so that $n$ is basically constant on these intervals.
Using @Martin.s's approach,
$$\mathbb{E}[\,k^{-\left|\sin (k)\right|}] =\frac{2}{\pi}\int_0^1 e^{-x\log(k)}\frac{dx}{\sqrt{1-x^2}}=I_0(\log (k))-\pmb{L}_0(\log (k))$$ where Bessel and Struve functions appear. $$\mathbb{E}[\,k^{-\left|\sin (k)\right|}] =\frac{2}{\pi^2 \log (k)}\sum_{n=0}^\infty\frac {4^n \,\Gamma \left(n+\frac{1}{2}\right)^2 } {\log^{2n}(k) }$$ Similarly, with $t=\log(k)$, $$\frac{I_0(t)-\pmb{L}_0(t)}{\log (t)}=\frac{2}{\pi \, t \log (t)}\Bigg(1+ \frac 1{t^2}+\frac 9{t^4}+O\left(\frac{1}{t^6}\right)\Bigg)$$
