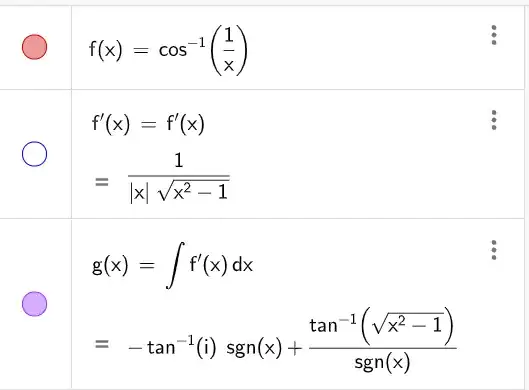I'm currently using Geogebra 6.0.791.0 and I ran into a strange result while trying to integrate the derivative of the $\sec^{-1}(x) = \cos^{-1}(\frac{1}{x})$ function.
The first differentiation is correct since:
$\frac{d}{dx}\sec^{-1}(x) = \frac{d}{dx}\cos^{-1}(\frac{1}{x}) = \frac{1}{|x|\sqrt{x^2-1}}$
But when I let it integrate this result it doesn't get back to $\sec^{-1}(x)$, instead it gives a dubious answer that can't even be graphed.
In this answer, the second summand is actually correct on its own since:
$\newcommand{\sgn}{\text{sgn}}$ $\frac{d}{dx} \sgn(x)\tan^{-1}(\sqrt{x^2-1}) = \sgn(x)\frac{1}{1+(\sqrt{x^2-1})^2} \frac{x}{\sqrt{x^2-1}} = \frac{1}{|x|\sqrt{x^2-1}}$
But the first summand is definitely wrong since $\tan^{-1}(i)$ has no solutions.
I think it still considers the whole sum as a valid antiderivative because it most likely assumes that undefined times zero equals zero:
$\frac{d}{dx}\tan^{-1}(i)\sgn(x) =\tan^{-1}(i) \frac{d}{dx}\sgn(x) = \tan^{-1}(i)\cdot 0 = 0$
I know this isn't a Geogebra support page, but I'm curious what mathematical reasoning led to the wrong solution, especially the $\tan^{-1}(i)$ part.