Consider a triangle $ABC$ and a point $T$. Given that $∠ATB=∠ATC=∠BTC=120°$ and $AC=3$, $BC=4$, $∠ACB=90°$, find $(9BT + 7CT)/AT$.
From the question we can imply that the point $T$ is the Fermat-Torricelli point of the triangle. The question wants us to basically find the distance from the vertex to this fermat's point .I have tried applying law of cosines but unable to solve further.
For convenience, let
$a=AT$
$b=BT$
$c=CT$
In $\triangle ACT, \triangle BCT, \triangle ABT$ the cosine rule gives
$a^2+c^2+ac=9$
$b^2+c^2+bc=16$
$a^2+b^2+ab=25$
Since $9+16=25$ we have
$(a^2+c^2+ac)+(b^2+c^2+bc)=(a^2+b^2+ab)$
$2c^2+ac+bc-ab=0$
Multiply both sides by $(a-b)$.
$(2c^2+ac+bc-ab)(a-b)=0$
Rearrange.
$(b^2+c^2+bc)(a-c)-(a^2+c^2+ac)(b-c)=0$
$16(a-c)-9(b-c)=0$
$\dfrac{9b+7c}{a}=16$
$\dfrac{9BT+7CT}{AT}=16$
Consider a generic right triangle $\triangle ABC$ right angle at $C$. Define $a := |BC|$, $b := |CA|$, $c := |AB|$ as usual. Let $A'$, $B'$, $C'$ complete external equilateral triangle $\triangle A'BC$, $\triangle AB'C$, $\triangle ABC'$.
It is "known" that lines $AA'$, $BB'$, $CC'$ concur at the Fermat-Torricelli point $T$. Define $p := |TA|$, $q := |TB|$, $r := |TC|$.
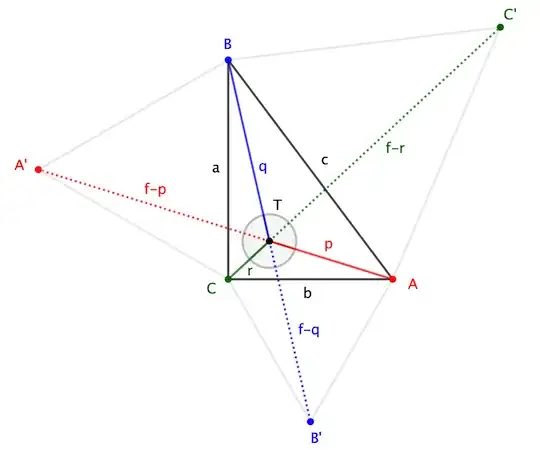
Pivoting $\triangle ACA'$ about $C$ causes it to align with $\triangle B'CB$; likewise at other vertices. This implies $|AA'|=|BB'|=|CC'|$; call the common length $f$. (The length is readily calculated —see Note 3 below— but turns out to be irrelevant here, as it will cancel on the way to the final expression.)
Let's setup a system of equations calculating the areas of "$|\triangle ABC| + \text{equilateral}$":
$$\begin{align} |\triangle ABC| + |\triangle A'BC| &= |\triangle ABA'|+|\triangle ACA'| = \frac12 f ( q + r )\sin 60^\circ \tag1\\ |\triangle ABC| + |\triangle AB'C| &= \phantom{|\triangle ABA'|+|\triangle ACA'|} = \frac12 f ( r + p )\sin 60^\circ \tag2 \\ |\triangle ABC| + |\triangle ABC'| &= \phantom{|\triangle ABA'|+|\triangle ACA'|} = \frac12 f ( p+q )\sin 60^\circ \tag3 \end{align}$$
These equations become
$$\begin{align} 2ab + a^2\sqrt{3} &= f ( q+r )\sqrt{3} \tag4\\ 2ab + b^2\sqrt{3} &= f ( r+p )\sqrt{3} \tag5 \\ 2ab + c^2\sqrt{3} &= f ( p+q )\sqrt{3} \tag6 \end{align}$$
Solving for $p$, $q$, $r$, and simplifying with $a^2+b^2=c^2$ gives
$$ p = \frac{b (a + b \sqrt{3})}{f \sqrt{3}} \qquad q = \frac{a (a \sqrt{3} + b)}{f\sqrt{3}} \qquad r = \frac{a b}{f\sqrt{3}} \tag7$$
For the problem at hand, we have $a=4$, $b=3$, $c=5$, so that $$ p = \frac{3 (4 + 3 \sqrt{3})}{f \sqrt{3}} \qquad q = \frac{4 (4 \sqrt{3} + 3)}{f\sqrt{3}} \qquad r = \frac{12}{f\sqrt{3}} \tag8$$
and we can calculate
$$\frac{9q+7r}{p} = \frac{36(4\sqrt{3}+3)+84}{3(4+3\sqrt{3})} = \frac{48(4+3\sqrt{3})}{3(4+3\sqrt{3})}= 16 \tag{$\star$}$$
I suspect there's an easier path to this result.
Note. Writing $(\star)$ as $$ 9 q + 7 r = 16 p$$ it's interesting that the coefficients on $p$, $q$, and $r$ are $a^2$, $b^2$, and $a+b$ ... but the last of these is a bit of an illusion: it's really $a^2-b^2$ (with the coincidence that $a-b=1$). The general relation might be written as
$$\frac{a^2}{q-r} = \frac{b^2}{p-r} \tag{$\star\star$}$$
Note 2. Even if we don't assume $a^2+b^2=c^2$, we still have that $(1-3)$ hold; the expression for $|\triangle ABC|$ doesn't reduce simply to $\frac12ab$, though.
Okay, so writing $|\triangle ABC|$ as the most-convenient form $\frac12bc\sin A$, $\frac12ca\sin B$, $\frac12ab\sin C$ as needed, we can find that
$$p:q:r \;=\; (1 + \cot A \sqrt3) : (1 + \cot B \sqrt3) : (1 + \cot C \sqrt3)$$
If we wanted, we could find $P$, $Q$, $R$ such that $$Pp+Qq+Rr=0$$ by having the "$1$" terms and "$\sqrt{3}$" terms vanish individually. After some simplification, we find $$\begin{align} P:Q:R &\;=\; (\cot B - \cot C) : (\cot C- \cot A) : (\cot A - \cot B) \\ &\;=\; \sin A \sin(B-C): \sin B \sin(C-A) : \sin C \sin(A-B) \end{align}$$
Note 3. In general, we have $$f^2 = \frac12\left(a^2+b^2+c^2+4\,|\triangle ABC|\,\sqrt{3}\right)$$
If we set: $\angle TCA=\alpha$, $TA=a$, $TB=b$, $TC=c$, the sine rule gives: $$ {3\over\sin120°}={a\over\sin\alpha}={c\over\sin(60°-\alpha)}, \quad {4\over\sin120°}={b\over\sin(90°-\alpha)}={c\over\sin(\alpha-30°)}. $$ This is a system of four equations in four unknowns. Solving for $\alpha$ is easy: from $$ c\sin120°=4\sin(\alpha-30°)=3\sin(60°-\alpha) $$ one gets $$ \tan\alpha={24+7\sqrt3\over39}. $$ But finding $a$, $b$, $c$ proves to be quite cumbersome. I used Mathematica and won't report here the results. which are a bit involved. But when I used those results to compute $(9b+7c)/a$, after simplification I got exactly $16$.
I think then there should be a simpler way to obtain that number.
COMMENT.-There is a unique point $T$ situated inside the given triangle $\triangle{ABC}$ of sides $3,4,5$ which is the intersection of the three locus from each of them one has $\angle{ATB}=\angle{ATC}=\angle{BTC}=120^{\circ}$ and the determination of the position of $T$ is the true problem here. A tedious enough calculation gives $T=(3.094,1.381)$ which is an approximation (that is not given by DESMOS).
Keeping in main this, what remains is easy with $A=(0,0),B=(3.2,2.4),C(5,0)$. We have $$\frac{9BT+7CT}{AT}\approx 7.58409039197$$
