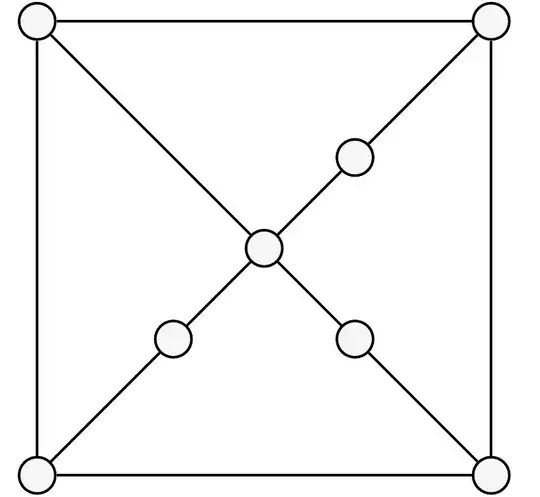
Consider a graph $H \cong K_{\ell} + (\ell - 1)K_1$ for $\ell \ge 3$ that has $\ell$ universal vertices and $(\ell - 1)$ vertices with no neighbors other than these universal vertices. Now replace every vertex of your example $G$ by a copy of $H$, and every edge by $\ell^2$ edges between the universal vertices of the corresponding copies of $H$. Now we have a graph $G'$ with $8(2\ell - 1)$ vertices and $11 \ell^2 + 12\ell(\ell - 1)$ edges.
The graph $G'$ is $\ell$-connected, because $H$ is $\ell$-connected and $\ell$ vertices of each copy of $H$ are adjacent to at least $\ell$ vertices of other copies (and yes, graph $G$ is connected).
The graph $G'$ is non-Hamiltonian. Suppose the opposite, that there is a Hamiltonian cycle $C'$. Then vertices of each copy of $H$ make exactly one contiguous subsequence of cyclic sequence of vertices corresponding to $C'$. This comes from two facts: 1) each of $(\ell - 1)$ non-universal vertices of the copy of $H$ is surrounded by two universal vertices of the same copy; 2) the number of universal vertices is greater than the number of non-universal vertices exactly by $1$. Thus we can contract vertices of each copy of $H$ into one, corresponding to a vertex of $G$. Note that adjacent vertices of different copies of $H$ correspond to adjacent vertices of $G$. Therefore the Hamiltonian cycle $C'$ of graph $G'$ turns to a Hamiltonian cycle $C$ of the graph $G$. This controversy proves the initial statement.
And the last (but not the least), $c(G' - S') \le |S'|$ for any $S' \subset V(G')$. If less than $\ell$ vertices are deleted from a copy of $H$ then it remains connected itself and connected to the same other copies of $H$. Removing $\ell$ universal vertices of a copy of $H$ produces $\ell - 1$ isolated vertices and has (in sense of components) the same effect on the remaining graph as removing a vertex of $G$ from $G$. So every $S' \subset V(G')$ corresponds to some $S \subset V(G)$. Therefore
$$\begin{aligned}c(G' - S') &\le (\ell - 1) \cdot \left\lfloor\frac{|S'|}{\ell}\right\rfloor + c(G - S)\\
&\le (\ell - 1) \cdot \left\lfloor\frac{|S'|}{\ell}\right\rfloor + |S|\\
&\le (\ell - 1) \cdot \left\lfloor\frac{|S'|}{\ell}\right\rfloor + \left\lfloor\frac{|S'|}{\ell}\right\rfloor\\
&= \ell \cdot \left\lfloor\frac{|S'|}{\ell}\right\rfloor \le |S'|.\end{aligned}$$