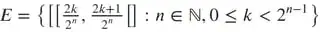0

Consider the Borel sigma-algebra on $\mathbb{R}$ quotiented by the ideal of measure-zero sets (see definitions below). This forms a measure algebra. My question is whether this measure algebra is countably generated, and I appear to have reached conflicting results.

Countably generated. This post suggests that the above is countably generated:

"One idea to provide a counter example is the following, let $\mathbb B([0,1[)$ be the Borel sets on $[0,1[$ and let $\lambda$ be the Lebesgue measure on $\mathbb B([0,1[)$. Then for $A,B\in \mathbb B([0,1[)$ define the equivalence relation $\lambda(A\triangle B)=0$, then if we let $A$ be the set of equivalence class of $\mathbb B([0,1[)$ modulo this equivalence relation. Denote by $[A]$ the equivalence class of $A$ and let $p([A])=\lambda(A)$. Then we can show that $p$ is positive and that $A$ is a Boolean $\sigma$-algebra with the countable chain condition. I think that the set

enter image description here

might do it, this would mean that the statement is true for at least one uncountable boolean algebra satisfying the requirements."

(Couldn't get mathjax to render the above correctly...)

Not countably generated. On the other hand, the Borel $\sigma$-algebra quotient null sets seems to be pretty clearly atomless by the following argument: any non-empty set must have positive measure, and therefore contain an open set which contains a subset of smaller measure (edit: this argument doesn't work, but see Prop 3.3.14 here). This post then references the remark:

There is no atomless countably generated $\sigma$-algebra.

Which is a contradiction with the countable generation derivation above.

Can anyone spot the issue here? It's likely something subtle but I'm not seeing it.

psychicmachinist
  • 107
  • Edited for clarity. The non-empty set having positive measure is the first step to showing atomless-ness. Any non-empty set must have strictly positive measure as we are quotienting out by the sigma-algebra of measure zero sets. – psychicmachinist Jul 04 '23 at 09:23
  • This is probably stupid question, but how do you define quotient of sigma-algebra - what is underlying set? – mihaild Jul 04 '23 at 09:33
  • Sets of positve measure don't need to contain open sets – FShrike Jul 04 '23 at 09:43
  • 1
    But since the topology is countably generated, so too is the $\sigma$-algebra. It is definitely the case that the Borel algebra is $\sigma(F)$ for some countable set of sets $F$ – FShrike Jul 04 '23 at 09:44
  • @FShrike. Ah right, the cantor set is Borel and has no open subset. So that doesn't work, but it still feels like that the space needs to be atomic. Can there really be a set of positive measure with no subset of strictly smaller measure? I've never seen such a set. – psychicmachinist Jul 04 '23 at 09:51
  • The Lebesgue measure spaces on $[0,1]$ or $\Bbb R$ or $\Bbb R^n$, whatever, are all atomless – FShrike Jul 04 '23 at 09:51
  • @FShrike I believe that the typical Borel $\sigma$-algebra is countably generated, but I'm not exactly sure about what happens when we quotient out null sets. This space seems to have some counter intuitive properties -- every increasing subsequence of sets under inclusion must be countable for example. – psychicmachinist Jul 04 '23 at 09:53
  • @mihaild We define an equivalence of two sets in the sigma algebra if their symmetric difference has measure zero. – psychicmachinist Jul 04 '23 at 09:54
  • @FShrike So if we agree the measure space is atomless, then isn't there a contradiction with countable generation? "There is no atomless countably generated $\sigma$-algebra" – psychicmachinist Jul 04 '23 at 09:56
  • @psychicmachinist this is how we get algebraic structure (we can transfer union and intersection to equivalence classes). But $\sigma$-algebra is more than this, it also has underlying set (so we can check if some element from underlying set is in some element of $\sigma$-algebra), and proof you linked significantly uses this. – mihaild Jul 04 '23 at 09:59
  • @mihaild Ah I think I see what you mean. My understanding is that when we quotient by the null sets we pass to a purely algebraic structure, and our boolean algebra no longer corresponds to sets over the original space (by Stone's representation thm, it is isomorphic to some set field, but not necessarily subsets of $\mathbb{R}^n$). But I'm definitely no mathematician so I might be missing something. – psychicmachinist Jul 04 '23 at 10:12

1 Answers1

1

(see Tao's post for much better information on these structures)

Definitions:

Abstract Boolean $\sigma$-algebra is tuple $(B, \varnothing, \cdot^c, \cup, \cap, \subset)$ (here all elements interpreted as just symbols, without standard set-theoretical meaning), where $B$ is set, $\varnothing \in B$, $\cdot^c$ is unary operation on $B$, $\cup$ and $\cap$ are binary operations on $B$, and $\subset$ is binary predicate on $B$, such that necessary properties are satisfied.

Concrete Boolean $\sigma$-algebra is tuple $(X, B)$ where $B \subset 2^{X}$ and $(B, \varnothing, \cdot^c, \cup, \cap, \subset)$ (here all symbols have their usual set-theoretical meaning) is abstract $\sigma$-algebra.

Proof you linked proves there is no concrete atomless countably generated $\sigma$-algebra. However, quotient of concrete $\sigma$-algebra is not necessary isomorphic to any concrete $\sigma$-algebra (Tao shows it with essentially the same construction).

Stone representation theorem says that any abstract Boolean algebra is isomorphic to some concrete Boolean algebra. However, it is not necessary the case for $\sigma$-algebra.

mihaild
  • 17,674