On a problem similar to the Goat problem

Question

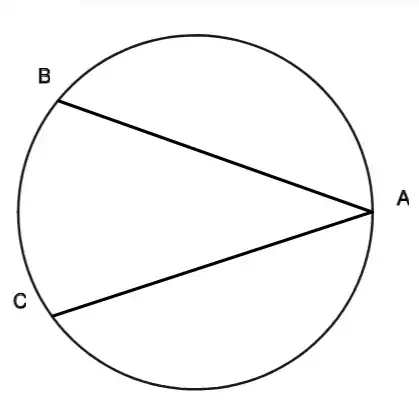
So I was trying to remember what the goat problem was when I thought of this:

Imagine points $A$, $B$, and $C$ on a circle. $B$ and $C$ are reflections of each other on the diameter that $A$ is on. What would $\theta=\angle BAC$ be if shape $BAC$ is half of the circle?

My idea was to let the center of the circle be $O$. We then draw radii $OB$, $OA$, and $OC$. Angle $BOC$ is $2\theta$ and angles $BOA$ and $COA$ are $\pi-\theta$. Using area formulas for triangles $ABO$ and $ACO$, we get $$r^2\sin\theta+\theta r^2=\frac{\pi}2r^2$$Where $r$ is the length of the radius. Dividing by $r^2$, we get stuck: $$\theta+\sin\theta=\frac{\pi}2$$ Are there other ways of reaching this equation, possibly even giving a closed form solution? I tried using Lagrange Inversion but the coefficients don't exist. Wolfram Alpha states that $\theta\approx48^\circ$ if this helps.

Answer 1

Since, by inspection, the solution is close to $\frac \pi 4$, you can write $$\theta+\sin(\theta)=\left(\frac{1}{\sqrt{2}}+\frac{\pi }{4}\right)+\left(1+\frac{1}{\sqrt{2}}\right)\left(\theta -\frac{\pi }{4}\right)+$$ $$\frac 1{\sqrt 2}\sum_{n=2}^\infty \frac { \sin \left(\frac{\pi n}{2}\right)+\cos \left(\frac{\pi n}{2}\right)}{n!} \left(\theta -\frac{\pi }{4}\right)^n$$

Truncation to some order and using power series reversion, $$\theta=\frac \pi 4 +\left(2-\sqrt{2}\right) \left(\frac{\pi }{4}-\frac{1}{\sqrt{2}}\right)+\left(5 \sqrt{2}-7\right) \left(\frac{\pi }{4}-\frac{1}{\sqrt{2}}\right)^2+$$ $$\left(50-\frac{106 \sqrt{2}}{3}\right) \left(\frac{\pi }{4}-\frac{1}{\sqrt{2}}\right)^3+\left(301 \sqrt{2}-\frac{1277}{3}\right) \left(\frac{\pi }{4}-\frac{1}{\sqrt{2}}\right)^4+\cdots$$ Using the above very truncated series, converted to decimal, in radians, the approximate result is $$\theta=\color{red}{0.8317111}77$$ while the "exact" solution is $0.831711194\dots$

Another solution could be to compute the first iterate of a Newton-like method of order $n$ to obtain $$\theta_{(2)}=1-\sqrt{2}-\frac{1}{4} \left(\sqrt{2}-3\right) \pi=0.83126019$$ $$\theta_{(3)}=\frac{32-44 \pi +\sqrt{2} (32+(\pi -24) \pi )}{4 \left(\sqrt{2} \pi -4 \left(7+4 \sqrt{2}\right)\right)}=0.83169998$$ and so on.

Edit

If you make $\theta=x+\frac \pi 2$, the equation becomes $$x+\cos(x)=0$$ and the solution is then $$t=\frac \pi 2 - \text{Dottie number}$$ $$t=\frac \pi 2 -\sqrt{1-\left(2 I_{\frac{1}{2}}^{-1}\left(\frac{1}{2},\frac{3}{2}\right)-1\right){}^2}$$ where appears the inverse of the regularized incomplete beta function.

This is the only closed form of the equation.

Answer 2

Kepler's equation is $M=E-e\sin E$, where $M$ is the mean anomaly, $E$ is the eccentric anomaly, and $e$ is the eccentricity.

Wikipedia https://en.wikipedia.org/wiki/Kepler%27s_equation says "solving for $E$ when $M$ is given can be considerably more challenging. There is no closed-form solution.

"One can write an infinite series expression for the solution to Kepler's equation using Lagrange inversion, but the series does not converge for all combinations of $e$ and $M$."

More information is given on that Wikipedia page and at the links given there.

Answer 3

Use

Kaplan, S. R. : The Dottie Number. Math. Mag. 80, 73-74,2007.

$$\theta=\sum_{n=0}^\infty\frac{\left(\frac\pi2\right)^{2n+1}}{(2n+1)!}\left.\frac{d^{2n}}{dx^{2n}}\left(1+\frac{\sin(x)}x\right)^{-(2n+1)}\right|_0$$

Unfortunately, applying the series reversion formula would be too complicated, $(y+1)^{-(2n+1)}=\sum\limits_{m=0}^\infty\frac{(-1)^m (m+2n)!}{(2n)!m!}y^m$ makes the coefficients diverge, and the top 2 formulas in the ratio section from Wolfram functions take too long to evaluate. However, as requested by the asker, one can find an integral representation a method with the inverse-Z transform:

$$\begin{align}\left.\frac{d^n}{dx^n}f(x)\right|_0=\frac{n!}{2\pi i}\int_{|z|=1}f(z)z^{-n-1}dz=\frac{n!}{2\pi}\int_0^{2\pi}f(e^{it})e^{-i nt}dt\implies \left.\frac{d^{2n}}{dx^{2n}}\left(1+\frac{\sin(x)}x\right)^{-(2n+1)}\right|_0=\frac{(2n)!}{2\pi}\int_0^{2\pi}\left(1+e^{-i t}\sin(e^{i t})\right)^{-(2n+1)}e^{-2nit}dt\end{align}$$

Summing over $n$ uses $\coth^{-1}$’s series expansion. After using integration by parts on $e^{i t}$ and the rest of the integrand, we get:

$$\boxed{\theta=\frac1{2\pi}\int_0^{2\pi}e^{it}\coth^{-1}\left(\frac2\pi(\sin(e^{it})+e^{i t}\right)dt=\int_0^{2\pi}\frac{e^{2it}(\cos(e^{it})+1)}{4(\sin(e^{i t})+e^{i t})^2-\pi^2}dt}$$

shown here.

---

Also, you can just use “Solve $x+\sin(x) = \frac\pi2$” and Bessel J:

$$\theta+\sin(\theta)=\frac\pi2\implies \theta=\frac\pi 2+2\sum_{n=1}^\infty\frac{\text J_n(-n)}{n} \sin\left(\frac{\pi n}2\right)=\frac\pi2+2\sum_{n=1}^\infty\left(\frac{J_{4n-1}(4n-1)}{4n-1}-\frac{J_{4n-3}(4n-3)}{4n-3}\right)$$

Answer 4

Another form:

$\theta={\frac {1}{2\pi }}\int _{0}^{\infty }\ln \left({\frac {2\pi \cosh(x)+\pi ^{2}}{x^{2}+\cosh ^{2}(x)}}+1\right)\,dx$