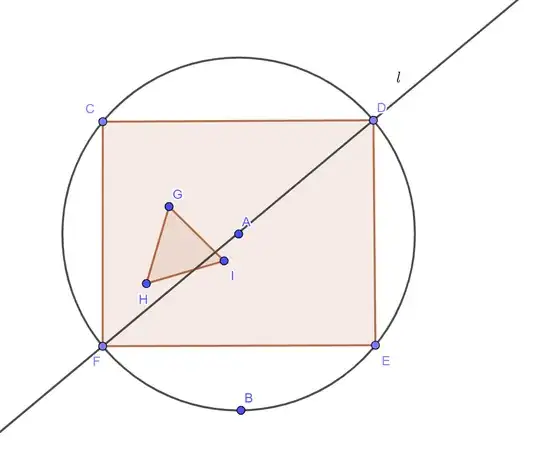
The pancake theorem guarantees that there is a line that can bisect a rectangle and a triangle simultaneously. The Borsuk Ulam Theorem can be used to prove that theorem. Show that any line through the center of a rectangle bisects the area of triangle simultaneously (the position of the center triangle can be the same as position the center of a rectangle or not)?