6

The base of a certain solid is the circle $x^2 + y^2 = a^2$.
Each plane perpendicular to the x-axis intersects the solid in a square cross-section with one side in the base of the solid.
Find its volume.

Here is my try :
$$y = \sqrt{a^2-x^2}$$
$$dV = (a^2-x^2)dx$$
$$V= 8\int_0^a (a^2-x^2)dx = \frac{16}{3}a^3$$
which is the correct answer given by textbook.

I know that solid has eight octants, for the book answer is $16a^3/3$,
Can someone help me understand why it has 8 octants, I integrate one part of the solid and then multiply by eight, why do I have to multiply by eight instead of four?

If the solids live above the z-axis then I have to multiply by four but in this case, how do I know the solid is also above the z-axis then multiply by eight

SirMrpirateroberts
  • 1,043

4 Answers4

3

The Question wording requires Multiplication by $4$ , not by $8$ . . . .

[[ EITHER the OP Integration is wrong (by the factor of $1/2$) & the wrong Multiplication by $8$ rather than $4$ somehow gives the right Answer (by giving the Extra factor $2$ thus cancelling the factor of $1/2$) OR the textbook may have a typo or error : Let us see which ]]

Earlier , My Answer was targeted towards whether (1) the Solid was in 4 Octants or 8 Octants & (2) whether to Multiply 1 Octant Volume by 4 or to Multiply 1 Octant Volume by 8 , assuming the OP did the Correct Integration.
I have updated my Answer to cover that Integration Itself , to verify what is going wrong where !

Here is the Image :

48

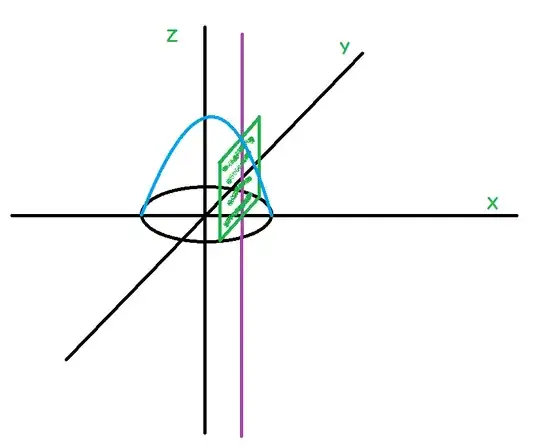
The Black Circle in $XY$ Plane is the BASE of the Solid.
Every Plane Perpendicular to $X$ Axis will get a Square Cross-Section (Shown in Green here) & we have to integrate that Square Area.
The TOP PART of the Solid (Shown in Blue) makes a Semi-Circle on the $XZ$ Plane. The Blue Curve will not be a Whole Circle , because the Black Circle is the BASE.
Thus we calculate in ONE Quadrant (ONE Octant) in $XY$ Plane & then Multiply that by $4$.

Imagine the Purple line going through the Solid & Parallel to the $YZ$ Plane & going through the $X$ Axis. The Solid Exists when $z$ Value is between $0$ & some Positive Value. There is no Solid when $z$ Value is Negative.

If the Black Circle was not the BASE but the Interior , then we might have a Different Integral with Different Criteria & we might have to multiply by $8$.

Integration :

The Square at Distance $x$ along the $X$ Axis has BASE Corners at $(x,+\pm \sqrt{a^2-x^2})$ , which gives width of the Square $2\sqrt{a^2-x^2}$ which is also the height of the Square.
Now , the Square is half in 1 Octant & half in other Octant. Thus Area in 1 Octant is $height \times width/2$ which is $2\sqrt{a^2-x^2} \times 2\sqrt{a^2-x^2}/2 = 2(a^2-x^2)$

We want to Integrate this in 1 Octant , thus $x$ is between $0$ & $a$.
Volume in 1 Octant is $\int_0^a 2(a^2-x^2) dx = [a^2x-x^3/3]_0^a = a^3-a^3/3=2a^3/3$
Volume in 4 Octants is $4 \times 2a^3/3 = 8a^3/3$

Thus we see that OP had 2 errors , which got cancelled to get the Correct Answer , by luck !

SUMMARY :

Assuming the Question wording is Accurate : You are right , you have to multiply by $4$ , but your Integration was having Extra factor $1/2$ & when you multiply by $8$ , it gives Extra factor $2$ which cancels the $1/2$ to get the text book Answer by luck.
In other words , $4 \times V \equiv 8 \times V/2$ & Everything is OK !

Prem
  • 14,696
  • A plane below the z axis in also perpendicular to x axis – SirMrpirateroberts Jun 17 '23 at 15:33
  • But then the Black Circle will not be the "BASE" of the Solid , @SirMrpirateroberts , When we have the Solid below $z=0$ , then we get the SPHERE where the "BASE" itself will be a DOT POINT. In that Case , we have to Multiply by $8$. In Current Case , we have to multiply by $4$. – Prem Jun 17 '23 at 15:47
  • 1
    thank you @Prem. – SirMrpirateroberts Jun 17 '23 at 16:06
  • The top part of the solid (shown in blue) instead makes half an ellipse on the $xz$-plane. For the square cross-section at a particular $x$, the side length on the base is $2\sqrt{a^2-x^2}$, which then becomes the $y$-coordinate of the blue curve: $y=2\sqrt{a^2-x^2}$. – peterwhy Jun 18 '23 at 01:05
  • But then such half an ellipse shape on the $xz$-plane can be reshaped more symmetrically to a full circle, using the Cavalieri's principle. Instead of having the square cross section with one side on the $xy$-plane, shift the cross sections down to have their centres on the $x$-axis. This moves volume to the $4$ octants below the $xy$-plane, and is what the OP was integrating (apart from the incorrect $\pi$ factor). – peterwhy Jun 18 '23 at 01:14
  • 1
    There does not appear to be any error in the book. The OP did the integration incorrectly. The correct answer is here: https://math.stackexchange.com/a/4720877/139123 – David K Jun 18 '23 at 03:30
  • I have updated my Answer , @DavidK , by doing the Integration myself : The Issue was [[ $4 \times 1 = 8 \times 1/2$ ]] , OP had 2 errors which got cancelled ! – Prem Jun 18 '23 at 05:35
  • I have updated my Answer , @peterwhy , by doing that Integration according to my Image , without shifting to 8 Octants : The OP Issue was [[ $4 \times 1 = 8 \times 1/2$ ]] & OP had 2 errors which got cancelled ! [[ OP had the $\pi$ wrong , though that might have been a typo ! ]] – Prem Jun 18 '23 at 05:45
3

For the square cross-section at a particular $x$, the side length on the base is $2\sqrt{a^2-x^2}$, so the cross-sectional area should be $4\left(a^2-x^2\right)$ -- $4\times$ what you used for $dV$.

$$dV = 4\left(a^2-x^2\right)dx$$

As the circular base goes from $x=-a$ to $x=a$, the limits of integration may instead be from $-a$ to $a$. This explains $2\times$ out of the scaling factor in your $V$.

These together explain the seemingly arbitrary $8\times$ scaling factor in your $V$.

$$\begin{align*} V &= \int_{-a}^a 4\left(a^2-x^2\right) dx\\ &= \int_{-a}^0 4\left(a^2-x^2\right) dx + \int_0^a 4\left(a^2-x^2\right) dx\\ &= \int_{a}^0 4\left(a^2-(-x)^2\right) d(-x) + \int_0^a 4\left(a^2-x^2\right) dx\\ &= \int_0^a 4\left(a^2-x^2\right) dx + \int_0^a 4\left(a^2-x^2\right) dx\\ &= 8\int_0^a \left(a^2-x^2\right) dx\\ &= 8\left[a^2x - \frac{x^3}{3}\right]_0^a\\ &= \frac{16}{3}a^3 \end{align*}$$

(Also, in an earlier version, you had an incorrect $\pi$ factor that got lost after incorrect integration.)

peterwhy
  • 22,930
0

Just like the $x-y$ plane has four quadrants,

  • $+x, +y$
  • $+x, -y$
  • $-x, +y$
  • $-x, -y$

the $x-y-z$ space has eight octants:

  • $+x, +y, +z$
  • $+x, +y, -z$
  • $+x, -y, +z$
  • $+x, -y, -z$
  • $-x, +y, +z$
  • $-x, +y, -z$
  • $-x, -y, +z$
  • $-x, -y, -z$
John
  • 26,582
  • Yea but how do I know this specific solid is in the eight spaces instead of just four see the question above – SirMrpirateroberts Jun 17 '23 at 14:57
  • By stating that the figure is a solid, the implication is that it exists in physical three-dimensional space. (Well, it would exist if it had weight and all that.) – John Jun 17 '23 at 15:00
  • see this answer I have to multiply by four instead of 8 https://math.stackexchange.com/a/4720254/1177689 – SirMrpirateroberts Jun 17 '23 at 15:01
  • Ahh, OK. I see where you're coming from. The other question talks about a "tent" which only goes from the ground up. That uses four octants because you don't consider the $-z$ direction. Now we go here and the question talks about a "base" just like the base of the tent in the other question. All I can tell you is that base doesn't mean the same thing in both questions, unfortunately. – John Jun 17 '23 at 15:05
  • 1
    Each plane perpendicular to the x-axis intersects the solid in a square cross-section with one side in the base of the solid, is in that sentence explained why solid is also below z axis? – SirMrpirateroberts Jun 17 '23 at 15:08
  • I think you figured it out! That seems to be exactly why. – John Jun 17 '23 at 15:11
  • thats the question, but I dont undestand – SirMrpirateroberts Jun 17 '23 at 15:12
  • 1
    The four octants below the $x,y$ plane are irrelevant. The entire solid has only non-negative $z$ coordinates, but the OP did the integration incorrectly. The correct answer is here: https://math.stackexchange.com/a/4720877/139123 – David K Jun 18 '23 at 03:29
-1

The answer is straightforward. Coordinates $x$ and $y$ will only have positive or negative signs. That means they can have up to 4 variations, the same as in quadrants. Therefore, if we put another coordinate $z$, number of possibilities increases to 8, as $2^3 = 8$

Possibilities are:

  • $+x,+y,+z$
  • $+x,+y,−z$
  • $+x,−y,+z$
  • $+x,−y,−z$
  • $−x,+y,+z$
  • $−x,+y,−z$
  • $−x,−y,+z$
  • $−x,−y,−z$
Sarich
  • 35