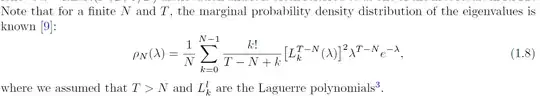A closed form expression for the marginal probability density of eigenvalues of real Wishart matrices

Question

This is a follow-up to my other question here . Define ${\mathfrak a}:= (T-N-1)/2 \in {\mathbb N}$ for $T > N+1$ and both $N,T \in {\mathbb N} $. Go to the link for the definition of the prefactor ${\mathfrak P}_{N,T}$. As explained in the aforementioned link the Laplace transform of the marginal pdf of the eigenvalues of real Wishart matrices reads:

\begin{eqnarray} E\left[ e^{-s \lambda} \right] = \frac{{\mathfrak P}_{N,T}}{N} 2^{\binom{N+1}{2} + N {\mathfrak a}} \cdot \sum\limits_{J=1}^N \prod\limits_{j=1}^N \left( \partial_i + \cdots + \partial_N \right)^{\mathfrak a} \cdot \prod\limits_{1 \le i < j \le N} \left( \partial_i + \cdots + \partial_{j-1} \right) \cdot \left. \frac{1}{x_1 x_2 \cdots x_N} \right|_{x_j \rightarrow j + 2 s 1_{j \ge J}} \tag{1} \end{eqnarray}

By using the techniques from the aforementioned link we obtained a closed form result for $N=3$ and then we inverted it to obtain the marginal pdf of the eigenvalues $\rho_3(\lambda)$. It reads:

\begin{eqnarray} &&\rho_3(\lambda) = \frac{T}{2} \frac{{\mathfrak P}_{N,T}}{N} 2^{\binom{N+1}{2} + N {\mathfrak a}} \sum\limits_{\begin{array}{lll} k_1=0,\cdots,{\mathfrak a} \\ k_2=0,\cdots2 {\mathfrak a} - k_1 \\ \theta=1,2 \end{array}} \binom{{\mathfrak a}}{k_1} \binom{2{\mathfrak a}-k_1}{k_2} \left( \right. \\ && \left. (-1)^{3 {\mathfrak a}+3} (k_2+3-\theta)!(3{\mathfrak a}-k_1-k_2)! \underline{\sum\limits_{l={\mathfrak a}}^{k_1+\theta} \binom{k_1+\theta}{l} {\mathfrak A}_{k_1,k_2}^{(\theta)} \cdot \left( - \frac{T \lambda}{2}\right)^l }\cdot e^{-\frac{1}{2} \lambda T} + \right. \\ && \left. (-1)^{3 {\mathfrak a}+3} (k_1+\theta)! (3{\mathfrak a}-k_1-k_2)! \underline{\sum\limits_{l={\mathfrak a}}^{k_2+3-\theta} \binom{k_2+3-\theta}{l} {\bar {\mathfrak A}}_{k_1,k_2}^{(\theta)} \cdot \left( - \frac{T \lambda}{2}\right)^l }\cdot e^{-\frac{2}{2} \lambda T} + \right. \\ && \left. (-1)^{k_2+\theta+1} (k_1+\theta)! (3{\mathfrak a}-k_1-k_2)! \underline{\sum\limits_{l={\mathfrak a}}^{k_2+3-\theta} \binom{k_2+3-\theta}{l} (1+3 {\mathfrak a}-k_1-k_2)^{(k_2+3-\theta-l)} \cdot \left( - \frac{T \lambda}{2}\right)^l }\cdot e^{-\frac{2}{2} \lambda T} \right. \\ && \left. \right) \tag{2} \end{eqnarray} Below there is a Mathematica code snippet that does the usual sanity checks, i.e. verifies that the (positve) moments of the pdf in $(2)$ are correct and then plots the pdfs in question for different values of $T$ in an ascending order from violet to red respectively. Here we go:

(*The same as above for N=3.*)
Clear[mLpTf]; NN = 3; k1 =.; lmb =.; k2 =.; k3 =.; s =.; T =.; 
mLpTf[T_] := 
 With[{aa = (T - NN - 1)/2}, 
  Pfct[NN, T]/NN 2^(Binomial[NN + 1, 2] + NN aa)
    Sum[ Binomial[aa, k1] Binomial[2 aa - k1, k2] (
          (k1 + th)!/(1 + 2 s/T)^(
         k1 + 1 + th) (k2 + 3 - th)!/(2 + 2 s/T)^(
         k2 + 1 + 3 - th) (k3)!/(3 + 2 s/T)^(k3 + 1) +
        (k1 + th)!/(1)^(k1 + 1 + th) (k2 + 3 - th)!/(2 + 2 s/T)^(
         k2 + 1 + 3 - th) (k3)!/(3 + 2 s/T)^(k3 + 1) +
        (k1 + th)!/(1)^(k1 + 1 + th) (k2 + 3 - th)!/(2)^(
         k2 + 1 + 3 - th) (k3)!/(3 + 2 s/T)^(k3 + 1)) /. 
     k3 :> 3 aa - k1 - k2, {k1, 0, aa}, {k2, 0, 2 aa - k1}, {th, 1, 
     2}]];
(*Sanity check. do positive moments match?*)
ll = Table[
   Normal@Series[mLpTf[NN + 1 + 2 Xi], {s, 0, 4}], {Xi, 0, 10}];
CoefficientList[ll, s] - 
 Table[With[{T = NN + 1 + 2 Xi}, {1, -1, 
    1/2! (1 + 4/T), -1/3! (1 + 22/T^2 + 12/T), 
    1/4! (1 + 164/T^3 + 126/T^2 + 24/T)}], {Xi, 0, 10}]
(Invert Laplace transform.)
Clear[mrho]; a1 =.; a2 =.; a3 =.;
mrho[T_, lmb_] := 
  With[{aa = (T - NN - 1)/2}, 
   T/2 Pfct[NN, T]/NN 2^(Binomial[NN + 1, 2] + NN aa)
     Sum[ Binomial[aa, k1] Binomial[2 aa - k1, k2] (
          (-1)^(
         3 aa + 3) (k2 + 3 - th)! (3 aa - k1 - k2)! Sum[
          Binomial[k1 + th, 
            l] (D[1 /( (a1 - 2)^(1 + k2 + 3 - th) (a1 - 3)^(
               1 + 3 aa - k1 - k2)), {a1, k1 + th - l}] /. 
             a1 :> 1) (-T/2 lmb)^l, {l, aa, k1 + th}] E^(-(1/2)
            1 lmb T) +
        (-1)^(
         3 aa + 3) (k1 + th)! (3 aa - k1 - k2)! Sum[
          Binomial[k2 + 3 - th, 
            l] (D[1/((a2 - 1)^(1 + k1 + th) (a2 - 3)^(
               1 + 3 aa - k1 - k2)), {a2, k2 + 3 - th - l}] /. 
             a2 :> 2) (-T/2 lmb)^l, {l, aa, k2 + 3 - th}] E^(-(1/2)
            2 lmb T) +
        (-1)^(-k2 - th - 1) (k1 + th)! (3 aa - k1 - k2)! Sum[
          Binomial[k2 + 3 - th, l] Pochhammer[1 + 3 aa - k1 - k2, 
            k2 + 3 - th - l] (-T/2 lmb)^l, {l, aa, k2 + 3 - th}] E^(-(
           1/2) 2 lmb T) ), {k1, 0, aa}, {k2, 0, 2 aa - k1}, {th, 1, 
      2}]];
(Test whether moments match.)
Xi = RandomInteger[{1, 15}];
mrho[NN + 1 + 2 Xi, lmb] // Expand;
Table[Integrate[lmb^p (%), {lmb, 0, Infinity}], {p, 0, 4}] - 
 With[{T = NN + 1 + 2 Xi}, {1, 1, 1 + 4/T, 1 + 22/T^2 + 12/T, 
   1 + 164/T^3 + 126/T^2 + 24/T}]
(Plot the marginal densities.)
num = 10;
lmb = Array[# &, 50, {0, 5}];
ListPlot[Table[
  Transpose[{lmb, mrho[NN + 1 + 2 Xi, lmb]}], {Xi, 0, num}], 
 PlotStyle -> Table[ColorData["Rainbow", i/(num)], {i, 0, num}], 
 Joined :> True, PlotMarkers -> Automatic, 
 AxesLabel :> {"lambda", "pdf"}, PlotLabel :> "N=" <> ToString[NN]]

---

Clearly the result is correct because the spectral moments match those being computed in a different way. However, this result does not match with equation (1.8) page 7 in

Bun, Joël; Bouchaud, Jean-Philippe; Potters, Marc, Cleaning large correlation matrices: tools from random matrix theory, Phys. Rep. 666, 1-109 (2017). ZBL1359.15031.

where the authors give a result that is supposed to be valid for all values of $N$ and $T$, a result that is incorrect (for various reasons-- firstly, their function can be bi-modal which is not how it should be and secondly it is not even normalized to unity). The authors give the following expression for the marginal pdf of the eigenvalues:

In view of all this my question is two fold, firstly where does the result from the aforementioned paper come from and can it be salvaged? The second question is obvious, i.e using our approach can we come up with a closed form expression for the marginal pdf of the eigenvalues for all values of $N$ and $T$.

Answer 1

Apart from a minor typo -- the quantity in the denominator should be $(T-N+k)!$ -- the formula in question is related to the Gaussian Unitary ensemble. I emailed the author of the paper and he told me that.

Now, we have derived the correct formula below. Here we used the theory as exposed in equation (12.22) and (12.23) in

Livan, Giacomo; Novaes, Marcel; Vivo, Pierpaolo, Introduction to random matrices. Theory and practice, SpringerBriefs in Mathematical Physics 26. Cham: Springer (ISBN 978-3-319-70883-6/pbk; 978-3-319-70885-0/ebook). ix, 124 p. (2018). ZBL1386.15003..

Define $a:= (T-N-1)/2$. Then define: $m_{i,j}:=4 \Gamma (a+i+1) \Gamma (a+j+1) \left(2^{2 a+i+j}-\frac{\, _2F_1(1,-a-i;a+j+2;-1) \Gamma (2 a+i+j+2)}{\Gamma (a+i+1) \Gamma (a+j+2)}\right)$ for $i,j=0,1,2,\cdots$.

We define auxiliary quantities as follows:

\begin{eqnarray} C_{2 k,\xi} &:=& (-1)^\xi \frac{\det \left[ \left( m_{\eta_1,\eta_2} \right)_{ \begin{array}{lll} \eta_1&=&0,\cdots,2k,\eta_1 \neq \xi \\ \eta_2&=&0,\cdots,2k,\eta_2 \neq 2k \end{array} } \right]}{ \det \left[ \left( m_{\eta_1,\eta_2} \right)_{ \begin{array}{lll} \eta_1&=&0,\cdots,2k+1,\eta_1 \neq 2k \\ \eta_2&=&0,\cdots,2k+1,\eta_2 \neq 2k+1 \end{array} } \right] } \quad \mbox{for $\xi=0,\cdots,2 k$}\\ %% C_{2 k+1,\xi} &:=& (-1)^\xi\frac{\det \left[ \left( m_{\eta_1,\eta_2} \right)_{ \begin{array}{lll} \eta_1&=&0,\cdots,2k+1,\eta_1 \neq 2 k \\ \eta_2&=&0,\cdots,2k+1,\eta_2 \neq \xi \end{array} } \right]}{ \det \left[ \left( m_{\eta_1,\eta_2} \right)_{ \begin{array}{lll} \eta_1&=&0,\cdots,2k+1,\eta_1 \neq 2k \\ \eta_2&=&0,\cdots,2k+1,\eta_2 \neq 2k+1 \end{array} } \right] } \quad \mbox{for $\xi=0,\cdots,2 k+1$} \end{eqnarray}

Then the spectral density reads:

\begin{eqnarray} \rho_N(x) &=& +x^a e^{-\frac{x}{2}} \frac{1}{N} \sum\limits_{k=0}^{N/2-1} \sum\limits_{\xi_1=0}^{2k+1} \sum\limits_{\xi_2=0}^{2k+1} \left( C_{2k,\xi_1} C_{2k+1,\xi_2} 1_{\xi_1 \le 2 k} - C_{2k+1,\xi_1} C_{2k,\xi_2} 1_{\xi_2 \le 2 k} \right) \cdot 2^{a+\xi_2+1} \cdot (a+\xi_2)! \cdot x^{\xi_1} + \\ &=&- x^a e^{-x} \frac{1}{N} \sum\limits_{k=0}^{N/2-1} \sum\limits_{\xi_1=0}^{2k+1} \sum\limits_{\xi_2=0}^{2k+1} \sum\limits_{\eta_2=0,\cdots,a+\xi_2} \left( C_{2k,\xi_1} C_{2k+1,\xi_2} 1_{\xi_1 \le 2 k} - C_{2k+1,\xi_1} C_{2k,\xi_2} 1_{\xi_2 \le 2 k} \right) \cdot 2^{2+\eta_2} \cdot (a+\xi_2)_{(\eta_2)} \cdot x^{\xi_1 + a+\xi_2-\eta_2} \tag{2} \end{eqnarray}

---

Now, we took $N,T = 4, 13$ we plotted the the quantity in $(2)$ and then we computed its first four integer moments numerically and compared them with results based on the Wick-Isserliss' theorem. As you can see the match is perfect.

Update:

We provide the code being used in the calculations above. It works for $N$ being even and $T \ge N + 3$ being odd.

Definitions:

(*Definitions*)
(For the definitions of the matrix elements m[i,j] and the 

coefficients CC[k,xi] see section (5.10) "Determinental 

Representations" page 101 in Mehta "Random matrices")
m[i_, j_] := 
  4 Gamma[1 + a + j] Gamma[
    1 + a + i] (2^(2 a + i + j) - 
     Gamma[2 + 2 a + i + j] /(Gamma[1 + a + i] Gamma[2 + a + j])
       Hypergeometric2F1[1, -a - i, 2 + a + j, -1]);
CC[0, 0] := 1/m[1, 0];
CC[k_, xi_] := (-1)^
    xi Det[Transpose[
       Drop[Transpose[
         Drop[Table[
           m[eta1, eta2], {eta1, 0, k}, {eta2, 0, k}], {1 + 
            xi}]], {1 + k}]]]/
     Det[Transpose[
       Drop[Transpose[
         Drop[Table[
           m[eta1, eta2], {eta1, 0, k + 1}, {eta2, 0, k + 1}], {1 + 
            k}]], {2 + k}]]] /; Mod[k, 2] == 0;
CC[k_, xi_] := (-1)^
    xi Det[Transpose[
       Drop[Transpose[
         Drop[Table[
           m[eta1, eta2], {eta1, 0, k}, {eta2, 0, k}], {1 + k - 
            1}]], {1 + xi}]]]/
     Det[Transpose[
       Drop[Transpose[
         Drop[Table[
           m[eta1, eta2], {eta1, 0, k}, {eta2, 0, k}], {1 + k - 
            1}]], {1 + k}]]] /; Mod[k, 2] == 1;
(The N being even case.)
rhoEven[x_] := 
  x^a Exp[-(x/2)] 1/
    NN  Sum[(If[xi1 <= 2 k, CC[2 k, xi1], 0] CC[2 k + 1, xi2] - 
        CC[2 k + 1, xi1] If[xi2 <= 2 k, CC[2 k, xi2], 0]) 2^(
      a + xi2 + 1) (a + xi2)! x^xi1, {k, 0, NN/2 - 1}, {xi1, 0, 
      2 k + 1}, {xi2, 0, 2 k + 1}] - 
   x^a Exp[-x] 1/
    NN  Sum[(If[xi1 <= 2 k, CC[2 k, xi1], 0] CC[2 k + 1, xi2] - 
        CC[2 k + 1, xi1] If[xi2 <= 2 k, CC[2 k, xi2], 0]) 2^(2 + eta2)
       Pochhammer[a + xi2 - eta2 + 1, eta2] x^(
      xi1 + a + xi2 - 
       eta2) (If[0 <= eta2 < IntegerPart[a] + xi2, 
        1, (2/x)^
         FractionalPart[a] Exp[x/2] Gamma[1 + FractionalPart[a], x/
          2]]), {k, 0, NN/2 - 1}, {xi1, 0, 2 k + 1}, {xi2, 0, 
      2 k + 1}, {eta2, 0, IntegerPart[a] + xi2}];

Verification of the skew-orthogonal polynomials:

(*Verify the R_2k[x] polynomials. *)
{NN, Xi} = {2, 2}; T = NN + 1 + 2 Xi;
a = (T - NN - 1)/2;
n =.; x =.; num = 8;
R2k1 = Table[
    Det[Join[{Table[x^eta1, {eta1, 0, 2 n}]}, 
       Transpose[
        Join[Table[
          m[eta1, eta2], {eta1, 0, 2 n - 1}, {eta2, 0, 
           2 n - 1}], {Table[m[2 n, eta2], {eta2, 0, 2 n - 1}]}]]]]/
     Det[Transpose[
       Drop[Transpose[
         Drop[Table[
           m[eta1, eta2], {eta1, 0, 2 n + 1}, {eta2, 0, 
            2 n + 1}], {1 + 2 n}]], {2 + 2 n}]]], {n, 0, num}] // 
   Expand;
R2k2 = Table[Sum[CC[2 n, eta] x^eta, {eta, 0, 2 n}], {n, 0, num}];
R2k1 - R2k2
(Verify the R_{2k+1}[x] polynomials. )
R2kp11 = Table[
    Det[Join[
       Table[m[eta1, eta2], {eta1, 0, 2 n - 1}, {eta2, 0, 
         2 n + 1}], {Table[x^eta1, {eta1, 0, 2 n + 1}]}, {Table[
         m[2 n + 1, eta2], {eta2, 0, 2 n + 1}]}]]/
     Det[Transpose[
       Drop[Transpose[
         Drop[Table[
           m[eta1, eta2], {eta1, 0, 2 n + 1}, {eta2, 0, 
            2 n + 1}], {1 + 2 n}]], {2 + 2 n}]]], {n, 0, num}] // 
   Expand;
R2kp12 = Table[
   Sum[CC[2 n + 1, eta] x^eta, {eta, 0, 2 n + 1}], {n, 0, num}];
R2kp11 - R2kp12

Main code:

{NN, Xi} = {4, 8}; T = NN + 1 + 2 Xi;
a = (T - NN - 1)/2;
x = Array[# &, 50, {1/10, 3}];
vals = Abs[( T rhoEven[# T] & /@ x)];
ListPlot[Transpose[{x, vals}]]
x =.; NIntegrate[{(x/T)^-2, (x/T)^-1, 
   1, (x/T)^1, (x/T)^2, (x/T)^3, (x/T)^4} Abs[rhoEven[x]], {x, 0, 
  Infinity}, WorkingPrecision -> 20]
N[{(T^2 (T - 
     1))/((Product[(T - NN + j), {j, 0, 
      0}]) (Product[(T - NN - 2 j - 1), {j, 0, 1}])), T/(-1 - NN + T),
   1, 1, 1 + (1 + NN)/T, 1 + (4 + 3 NN + NN^2)/T^2 + (3 + 3 NN)/T, 
  1 + (20 + 21 NN + 6 NN^2 + NN^3)/T^3 + (21 + 17 NN + 6 NN^2)/T^2 + (
   6 + 6 NN)/T}, 20]

Output: