Evaluate : $\int_0^{\frac{\pi}{2}} \frac{\ln(\sec ^2 x)\sec^2x }{(\sec ^2 x+1)\tan x}\mathrm dx$

Question

I need to evaluate :

$$I=\int_0^{\frac{\pi}{2}} \frac{\ln(\sec ^2 x)\sec^2x \mathrm dx}{(\sec ^2 x+1)\tan x}$$ By substituting $x\to \frac{\pi}{2} - x$ , I get :

$$I =\int_0^{\frac{\pi}{2}} \frac{\ln(\csc^2 x)\csc^2x \mathrm dx}{(\csc ^2 x+1)\cot x}$$

But I do not know how to proceed with this. I also tried the substitution $\tan x = u$ which transform $I$ to :

$$I = \int_0^\infty \frac{\ln(u^2 +1)\mathrm du}{u^3+ 2u}$$

But still I cannot proceed further from here because I have never solved such type of integrals with the limited techniques I know.

Answer 1

I claim that $$\int_0^{\frac{\pi}{2}} \frac{\ln(\sec ^2 x)\sec^2x \mathrm dx}{(\sec ^2 x+1)\tan x} = \frac{\pi^2}{16}.$$

We start with the substitution $\sec^2x = u$ to obtain $$\int_0^{\frac{\pi}{2}} \frac{\ln(\sec ^2 x)\sec^2x \mathrm dx}{(\sec ^2 x+1)\tan x} = \frac{1}{2}\int_1^{\infty}\frac{\ln(u)}{(u+1)(u-1)}\,du = \frac{1}{2}\int_1^{\infty} \frac{\ln(u)}{u^2-1}\,du.$$ Next make the substitution $u = 1/t$ to obtain $$\int_1^{\infty} \frac{\ln(u)}{u^2-1}\,du = -\frac{1}{2}\int_0^{1} \frac{\ln(t)}{1-t^2}\,dt$$ We can expand $1/(1-t^2)$ by its geometric series to get $$\int_0^1\frac{\ln(t)}{1-t^2} = -\frac{1}{2}\sum_{n=0}^{\infty}\int_0^1t^{2n}\ln(t)\,dt.$$ Making the substitution $y=-\ln(t)$ yields $$\int_0^1t^{2n}\ln(t)\,dt = -\int_0^{\infty}ye^{-(2n+1)y}\,dy.$$ Then $(2n+1)y = \alpha$ yields $$-\int_0^{\infty}ye^{-(2n+1)y}\,dy = -\frac{1}{(2n+1)^2}\int_0^{\infty}\alpha e^{-\alpha}\,d\alpha = -\frac{1}{(2n+1)^2},$$ where we evaluated the last integral using integration by parts. Hence $$-\frac{1}{2}\sum_{n=0}^{\infty}\int_0^1t^{2n}\ln(t)\,dt = \frac{1}{2}\sum_{n=0}^{\infty}\frac{1}{(2n+1)^2}.$$ The last sum has a well known value of $\pi^2/8$, which means $$\int_0^{\frac{\pi}{2}} \frac{\ln(\sec ^2 x)\sec^2x \mathrm dx}{(\sec ^2 x+1)\tan x} = \frac{\pi^2}{16}.$$ This agrees numerically with what desmos tells me.

Answer 2

Utilize $ \int_0^{\frac\pi2}\frac{\tan y}{\tan^2y+a^2}dy =\frac{\ln a}{a^2-1}$ with $a^2=\sec^4x$ to integrate \begin{align} &\int_0^{\frac{\pi}{2}} \frac{\ln(\sec ^2 x)\sec^2x}{(\sec ^2 x+1)\tan x}dx\\ =&\ \frac12 \int_0^{\frac{\pi}{2}} \int_0^{\frac\pi2} \frac{\tan y \tan x \sec^2x}{\tan^2y+\sec^4x}dy\ dx =\frac12 \int_0^{\frac\pi2}y \ dy=\frac{\pi^2}{16} \end{align}

Answer 3

Start from where the OP stuck, Let $$F(a)=\int_0^\infty \frac{\ln(1+au^2)}{u(u^2+2)}du\Longrightarrow F'(a)=\int_0^\infty \frac{u}{(u^2+2)(1+au^2)}du$$

So $F(0)=0$, then let $t=u^2$

$$F'(a)=\frac12\int_0^\infty \frac{1}{(t+2)(1+at)}dt=\frac{\ln(2a)}{2(2a-1)}$$ We get $$\int_0^\infty \frac{\ln(1+u^2)}{u(u^2+2)}du=F(1)=\int_0^1 \frac{\ln(2a)}{2(2a-1)}da$$

Let $x=2a$

$$F(1)=-\frac14\int_0^1 \frac{\ln(x)}{1-x}dx-\frac14\int_1^2 \frac{\ln(x)}{1-x}dx=\frac{\pi^2}{24}-\frac14\int_1^2 \frac{\ln(x)}{1-x}dx$$

Let $t=x-1$

$$F(1)=\frac{\pi^2}{24}+\frac14\int_0^1 \frac{\ln(1+t)}{t}dt$$

Integration by part, we get

$$F(1)=\frac{\pi^2}{24}-\frac14\int_0^1 \frac{\ln(t)}{1+t}dt=\frac{\pi^2}{24}+\frac{\pi^2}{48}=\frac{\pi^2}{16}$$

Answer 4

Let $u=\ln(\sec^2x)$ and then \begin{eqnarray} I&=&\int_0^{\frac{\pi}{2}} \frac{\ln(\sec ^2 x)\sec^2x \mathrm dx}{(\sec ^2 x+1)\tan x}\\ &=&\frac12\int_0^{\infty} \frac{ue^u}{e^{2u}-1}\mathrm du=\int_0^{\infty} \frac{ue^{-u}}{1-e^{-2u}}\mathrm du\\ &=&\frac12\int_0^{\infty}\sum_{n=0}^\infty ue^{-(2n+1)u}\mathrm du\\ &=&\frac12\sum_{n=0}^\infty\frac1{(2n+1)^2}=\frac{\pi^2}{16}. \end{eqnarray}

Answer 5

We make the substitution $x \mapsto \cos^2x$ to get

$$ I := \int_{0}^{\frac{\pi}{2}}\frac{\ln\left(\sec^{2}x\right)\sec^{2}x}{\left(\sec^{2}x+1\right)\tan x}dx=-\int_{0}^{\frac{\pi}{2}}\frac{\ln\left(\cos^{2}x\right)\cot x}{1+\cos^{2}x}dx=\frac{1}{2}\int_{0}^{1}\frac{\ln x}{x^{2}-1}dx. $$

Let $f(z) = \displaystyle\frac{\log z}{z^2-1}$ where $\operatorname{arg}(z) \in (-\pi,\pi]$ and the branch cut is on the negative real axis. The series expansion of $f(z)$ centered at $z=1$ is $\displaystyle \frac{1}{2}-\frac{z-1}{2}+\frac{5}{12}\left(z-1\right)^{2}+O\left(\left(z-1\right)^{3}\right)$, which tells us $z=1$ is a removable singularity.

Next, we traverse along the following contour in the positive direction.

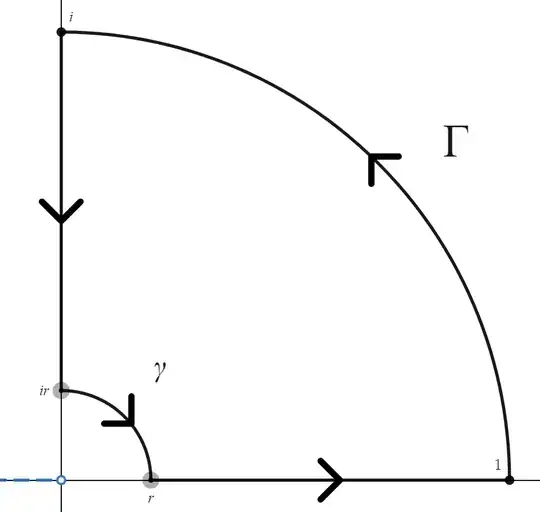
Cauchy's Residue Theorem allows us to write

$$ 0 = \left(\int_{r}^{1}+\int_{\Gamma}^{ }+\int_{i}^{ir}+\int_{\gamma}^{ }\right)f(z)dz. $$

Equating the real part on both sides gives us

$$ 0 = \int_{r}^{1}f(z)dz+\Re\int_{\Gamma}^{ }f(z)dz+\Re\int_{i}^{ir}f(z)dz+\Re\int_{\gamma}^{ }f(z)dz. $$

We evaluate each contribution and take $r \to 0^+$ below.

---

$$ \begin{align} I_2 &:= \Re\int_{\Gamma}^{ }f(z)dz \\ &= \Re\int_{0}^{\frac{\pi}{2}}\frac{\log\left(e^{i\theta}\right)}{\left(e^{i\theta}\right)^{2}-1}d\left(e^{i\theta}\right) \\ &= \Re\int_{0}^{\frac{\pi}{2}}\frac{ie^{i\theta}}{e^{2i\theta}-1}\log\left(e^{i\theta}\right)d\theta \\ &= \Re\int_{0}^{\frac{\pi}{2}}\frac{\csc\theta}{2}\left(\ln\left|e^{i\theta}\right|+i\operatorname{arg}\left(e^{i\theta}\right)\right)d\theta \\ &= \Re\frac{i}{2}\int_{0}^{\frac{\pi}{2}}\theta\csc\theta d\theta \\ &= 0 \\ \end{align} $$

---

$$ \begin{align} I_{3} &:= \Re\int_{i}^{ir}\frac{\log z}{z^{2}-1}dz \\ &= \Re\int_{1}^{r}\frac{\log\left(iy\right)}{\left(iy\right)^{2}-1}d\left(iy\right) \\ &= \Re i\int_{r}^{1}\frac{\log\left(iy\right)}{y^{2}+1}dy \\ &= \Re i\int_{r}^{1}\frac{\ln\left|iy\right|}{y^{2}+1}dy-\Re\int_{r}^{1}\frac{\operatorname{arg}\left(iy\right)}{y^{2}+1}dy \\ &= -\frac{\pi}{2}\int_{r}^{1}\frac{1}{y^{2}+1}dy \\ &\to -\frac{\pi}{2}\int_{0}^{1}\frac{1}{y^{2}+1}dy \\ &= -\frac{\pi^{2}}{8} \\ \end{align} $$

---

$$ \begin{align} I_4 &:= \int_{\gamma}f(z)dz \\ &= \int_{\frac{\pi}{2}}^{0}\frac{\log\left(re^{i\phi}\right)}{\left(re^{i\phi}\right)^{2}-1}d\left(re^{i\phi}\right) \\ &= ir\int_{0}^{\frac{\pi}{2}}\frac{e^{i\phi}\log\left(re^{i\phi}\right)}{1-r^{2}e^{2i\phi}}d\phi \\ &= ir\int_{0}^{\frac{\pi}{2}}\frac{e^{i\phi}\left(\ln\left|re^{i\phi}\right|+i\operatorname{arg}\left(re^{i\phi}\right)\right)}{1-r^{2}e^{2i\phi}}d\phi \\ &= ir\ln r\int_{0}^{\frac{\pi}{2}}\frac{e^{i\phi}}{1-r^{2}e^{2i\phi}}d\phi-r\int_{0}^{\frac{\pi}{2}}\frac{\phi e^{i\phi}}{1-r^{2}e^{2i\phi}}d\phi \\ &\to i\left(0\right)\int_{0}^{\frac{\pi}{2}}\frac{e^{i\phi}}{1-0^{2}e^{2i\phi}}d\phi-0\int_{0}^{\frac{\pi}{2}}\frac{\phi e^{i\phi}}{1-0^{2}e^{2i\phi}}d\phi \\ &= 0 \\ \end{align} $$

---

Hence,

$$ \begin{align} 0 &= \lim_{r \to 0^+}I_1 + 0 -\frac{\pi^2}{8} + 0 \\ \implies I &= \frac{\pi^{2}}{16}\\ \end{align} $$

and we're finished!

Answer 6

$$\newcommand{dilog}[1]{\operatorname{Li}_2\left(#1\right)} \begin{align*} I &= \int_0^{\tfrac\pi2} \frac{\ln\left(\sec^2x\right) \sec^2x}{(\sec ^2 x+1) \tan x} \, dx \\ &= \frac12 \int_0^\infty \frac{\ln(x+1)}{x(x+2)} \, dx \tag1 \\ &= \frac12 \left(\int_0^1 \frac{\ln(x+1)}{x(x+2)} \, dx + \int_0^1 \frac{\ln\left(\frac1x+1\right)}{\frac1x\left(\frac1x+2\right)} \, \frac{dx}{x^2}\right) \tag2 \\ &= \frac12 \int_0^1 \frac{\ln(x+1)}{x(x+2)} \, dx - \frac12 \int_0^1 \frac{\ln\frac x{x+1}}{2x+1} \, dx \\ &= -\frac{\ln2\ln3}4 - \frac{J\left(\frac13\right)+J\left(\frac12\right)}2 \tag3 \\ &= \ln\sqrt3 \operatorname{arcoth}3 + \ln\sqrt2 \operatorname{arcoth}2 - \ln\sqrt2 \ln\sqrt3 + \frac{\dilog{\frac12} - \dilog{-\frac12} + \dilog{\frac13} - \dilog{-\frac13}}4 \tag4 \\ &= \frac{\ln2 \ln3}4 + \frac12\dilog{\frac12} + \frac12\dilog{\frac13} - \frac18\dilog{\frac14} - \frac18\dilog{\frac19} \tag5 \\ &= \boxed{\frac{\pi^2}{16}} \tag6 \end{align*}$$

---

Steps

• $(1)$ substitute $x\mapsto\arctan\sqrt x$
• $(2)$ split up the integral at $x=1$ and substitute $x\mapsto\dfrac1x$ for $x\in[1,\infty)$
• $(3)$ integrate the first term by parts and substitute $\dfrac x{x+2}\mapsto x$ : $$\int_0^1 \frac{\ln(x+1)}{x(x+2)} \, dx = -\frac{\ln2\ln3}2 - \frac12 \int_0^1 \frac{\ln \frac x{x+2}}{x+1} \, dx = -\frac{\ln2\ln3}2 - \int_0^{\tfrac13} \frac{\ln x}{1-x^2} \, dx \quad ;$$ substitute $\dfrac{x+1}x\mapsto x$ in the second term : $$\int_0^1 \frac{\ln\frac x{x+1}}{2x+1} \, dx = \int_0^{\tfrac12} \frac{\ln x}{1-x^2} \, dx \quad ;$$ and write in terms of the parameterized integral, $$J(a) := \int_0^a \frac{\ln x}{1-x^2} \, dx \qquad (0<a<1)$$
• $(4)$ evaluate $J(a)$ : $$\begin{align*} J(a) &= \frac12 \ln a \ln \frac{1+a}{1-a} - \frac12 \int_0^a \frac{\ln(1+x) - \ln(1-x)}x \, dx \tag{1$'$} \\ &= \ln a \operatorname{artanh}a - \frac12 \sum_{n=1}^\infty \left(\frac{(-1)^{n+1}}n+\frac1n\right) \int_0^a x^{n-1} \, dx \tag{2$'$} \\ &= \ln a \operatorname{artanh}a - \frac12 \sum_{n=1}^\infty \frac{1-(-1)^n}{n^2} a^n \\ &= \ln a \operatorname{artanh}a + \frac{\dilog{-a}-\dilog a}2 \tag{3$'$} \end{align*}$$
• $(5)$ duplication formula $\dilog x + \dilog{-x} = \frac12 \dilog{x^2}$
• $(6)$ combine MathWorld's identities $(9)$, $(25)$, and $(27)$ in the right amounts to eliminate the logarithms, e.g. $$\begin{align*} \dilog{\frac12} &= \frac{\pi^2}{12} - \frac{\ln^22}2 \\ \dilog{\frac13} - \frac16 \dilog{\frac19} &= \frac{\pi^2}{18} - \frac{\ln^23}6 \\ \dilog{\frac14} + \frac13\dilog{\frac19} &= \frac{\pi^2}{18} + 2\ln2 \ln3 - 2\ln^22 - \frac{2\ln^23}3 \\[2ex] \implies \color{red}{\frac{\ln2\ln3}4} &= -\frac{\pi^2}{144} + \frac{\ln^22}4 + \frac{\ln^23}{12} + \frac18 \dilog{\frac14} + \frac1{24} \dilog{\frac19} \end{align*}$$

---

Steps for $J(a)$

• $(1')$ integrate by parts
• $(2')$ exploit the Maclaurin series for both logarithms
• $(3')$ definition of dilogarithm a.k.a. Spence's function