3

A squared rectangle is a rectangle dissected into squares. squared rectangles are called perfect if the squares in the tiling are all of different sizes and are positive integers. The smallest perfect squared rectangle is 33x32 in width and height. 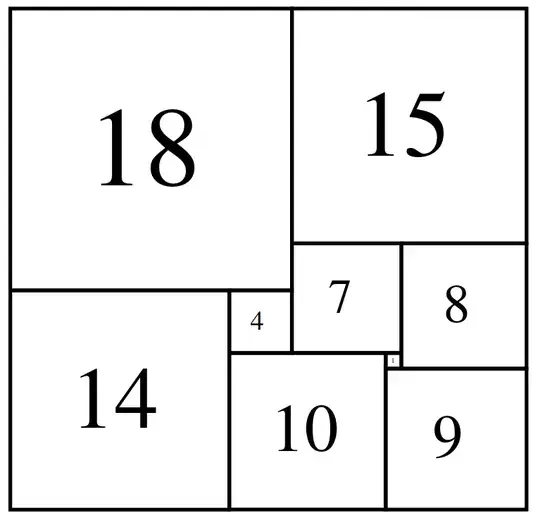enter image description here

The corners are the squares 18, 15, 14 and 9. 9 is the smallest known corner in a perfect squared rectangle. Millions of squared rectangles have been produced, this is the only known example of 9 in a corner. It is also the only known example of 14 in a corner. It is conjectured that 9 and 14 are only possible as corners in this arrangement. PSRs (perfect squared rectangles) have corners sizes from 15 upwards but only one example of a PSR with a corner of 11 is known. It was found by Brian Trial. http://www.squaring.net/sq/sr/spsr/51-773x661-11corner.pdf

The corresponding problem for the smallest square on the boundary has been solved by Ian Gambini. The smallest square possible on the boundary is 5. PSRs and PSSs (perfect squared squares) exist with squares on the boundary with sides of 5 and above. http://www.squaring.net/sq/sr/spsr/5-side-spss.png

Brian Trial also found 3 PSRs with 5 on the boundary http://www.squaring.net/sq/sr/spsr/o28-5-side.txt1pp.pdf (you need to zoom in to see the small squares)

No examples of PSRs with corners of 10, 12 and 13 are known.

Are they even possible?

I have generated whole orders of PSRs, over 300 million squared rectangles, all the way from order 9 up to 24 squares and have not found any with corners of 10,11,12,13. Brian Trial has different packing software and has found the order 51 PSR with the 11 corner but nothing else is known, to my knowledge.

Any suggestions, or useful software would be most welcome.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

UPDATE 2024 Brian's answers are quite amazing

Bouwkampcodes for SPSRs with corners of size 10,11,12,13 and 14 found by Brian are;

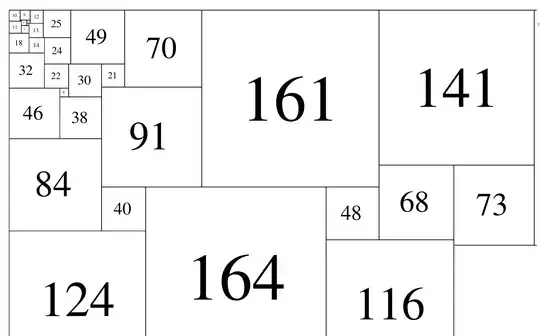
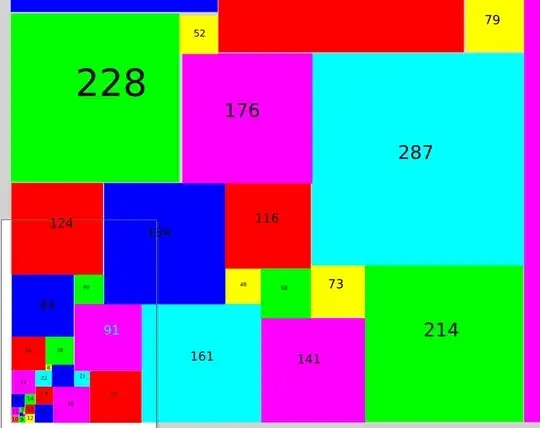
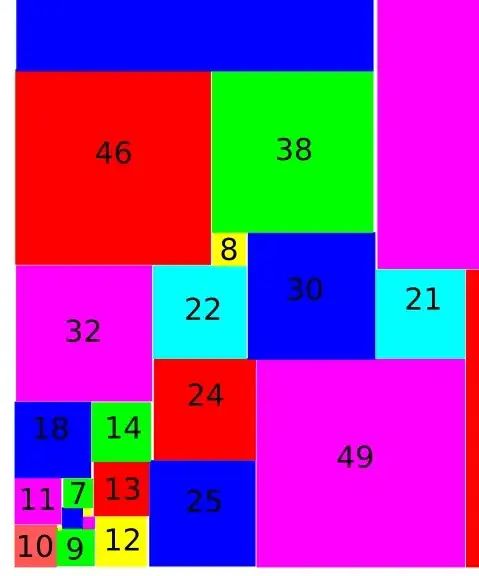
48 1271 1545 (712,559)(153,406)(280,332,253)(79,580)(228,52)(176,287)(124,164,116)(73,214)(48,68)(84,40)(91,161)(141)(46,38)(8,30)(32,22)(21,70)(24,49)(18,14)(13,25)(11,7)(5,2)(3,12)(10,1)(9)
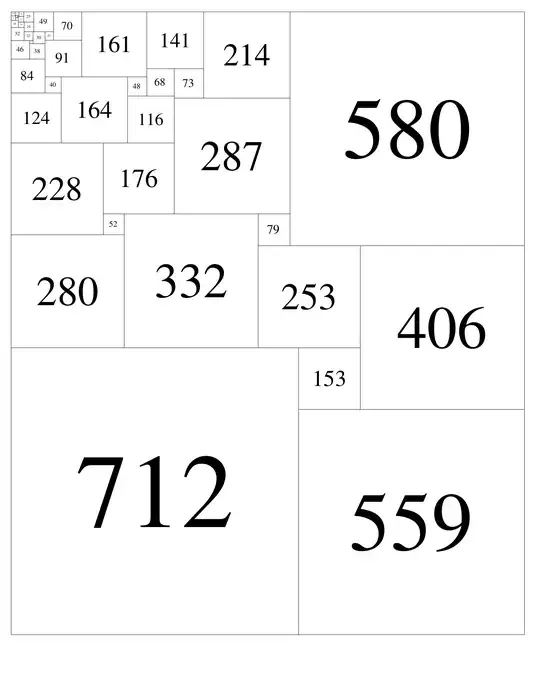
order 48 10 corner SPSR
48 1271 x 1545 , 10 corner zooming in.

48 1271 x 1545 , 10 corner zooming in.

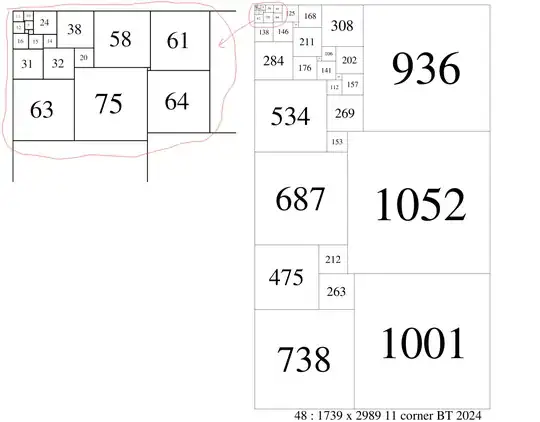
48 1739 2989 (11,10,24,38,58,61,125,168,308,936)(1,9)(12)(4,5)(16)(15,14)(32,20)(31)(75,3)(64)(63)(146,43)(138)(211)(284)(106,202)(176,35)(141)(45,157)(534,112)(269)(153,1052)(687)(475,212)(263,1001)(738)
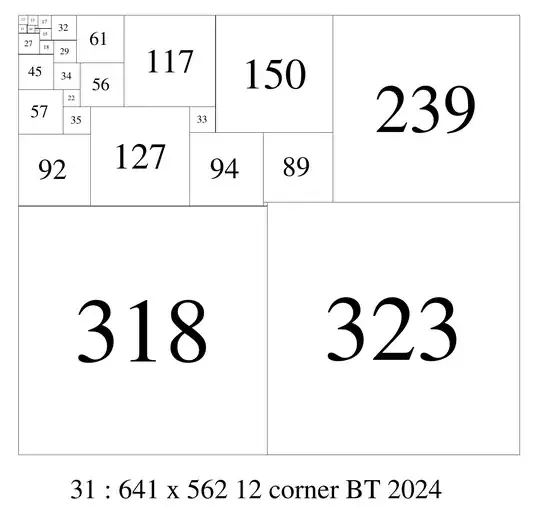
48 1739 x 2989 11 corner 31 641 562 (12,13,17,32,61,117,150,239)(11,1)(10,4)(6,15)(27)(18,29)(45)(34,56)(57,22)(35,127,33)(94,89)(92)(5,323)(318)
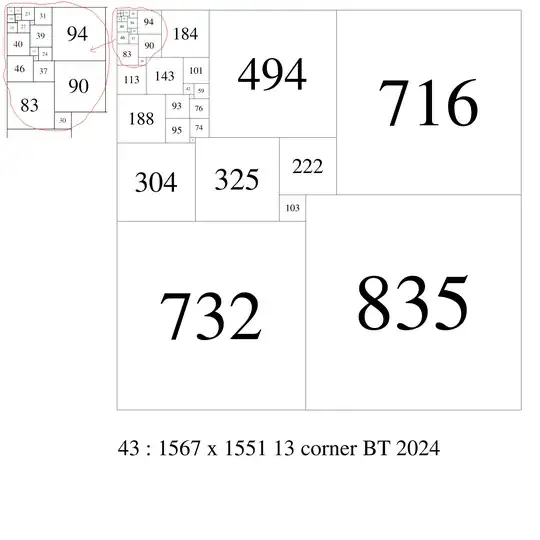
31 641 x 562 12 corner 43 1551 1567 (13,14,18,40,46,83,113,188,304,732)(12,1)(11,4)(22)(23)(8,39,15)(9,37)(31)(24)(94)(90,30)(143)(184)(93,95)(101,42)(17,76)(74,21)(59)(325)(494)(222,103)(835)(716)
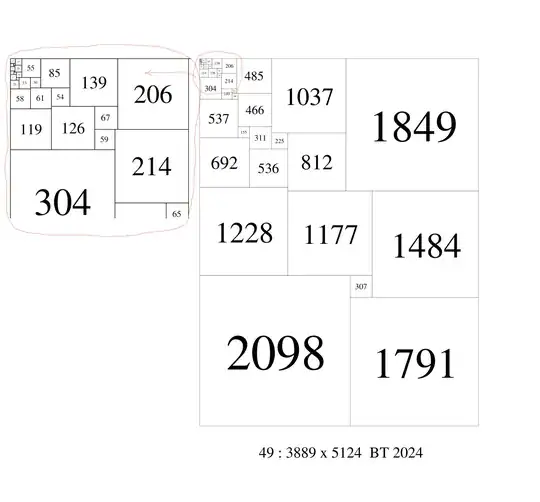
43 1551 x 1567 13 corner 49 5124 3889 (1849,1484,1791)(1177,307)(2098)(1037,812)(225,536,1228)(485,466,311)(155,692)(84,537)(206,214,65)(149)(139,67)(59,304)(126)(85,54)(61,119)(55,30)(33,58)(19,20,16)(8,25)(7,17)(14,5)(4,13,3)(10)(9)
49 5124 x 3889 14 corner

Stuart Anderson
  • 109

5 Answers5

2

I had long assumed that the only solution with 14 in the corner was the 33x32 rectangle you show above, but this is not the case!

Corner 14 Order 49 5124 x 3889

14 9 5 19 4 13 20 3 10 7 17 16 55 8 25 33 58 30 85 61 119 54 139 126 67 206 59 304 214 149 65 485 84 537 466 155 692 311 536 1228 225 1037 812 1849 1177 1484 307 2098 1791

Best Regards,

Brian Trial

Brian Trial
  • 394
2

enter image description here

1271x1545 SPSR with 10 in the corner.

Brian Trial
  • 394
2

enter image description here

Zoom in further..................

Brian Trial
  • 394
2

enter image description here

SPSR with 10 in the corner is based on this Ell, where subsequent squares are added by extending an edge of the Ell.

This Ell consists of squares 10,9,12,25,49,11,1,5,3,2,7,13,18,24,32,22,30,21,8,14,38,46

And the Ell extensions continue: 70,91,161,84,40,124,164,48,116,68,141,73,214,287,176,228,52,280,332,79,580,253,406,153,559,712 forming a 1271x1545 SPSR

Brian Trial
  • 394
1

My "Ell-grow" approach has yielded answers for 12 and 13, and a smaller order solution for 11. The problem is, I have the sequences of squares placed as the Ell grows, but no idea how to convert them to Bouwkamp code other than constructing these rectangles from scratch.

Here are the solutions:

Corner 11 Order 48 1739 x 2989

11 10 1 12 9 4 16 5 24 15 31 14 38 32 63 20 58 75 138 3 61 64 125 146 284 43 168 211 176 35 141 106 308 202 45 157 112 269 936 534 153 687 1052 212 475 263 738 1001

Corner 12 Order 31 562x641

12 11 1 13 10 4 17 6 27 15 32 18 45 29 61 34 56 117 22 57 35 92 127 33 150 94 89 239 5 318 323

Corner 13 Order 43 1567 x 1551

13 12 1 14 11 23 4 18 22 40 8 31 39 15 24 94 9 46 37 83 90 184 30 113 143 101 42 59 17 76 93 188 95 74 494 21 304 325 222 716 103 732 835

Best Regards, Brian Trial

Brian Trial
  • 394