The classical definition of a field $K$ with an absolute value $|\cdot|:K\to \mathbb{R}_{\geq 0}$ is that $\forall x,y\in K$
- $x=0\Leftrightarrow|x|=0$
- $|xy|=|x|\cdot|y|$
- $|x+y|\leq |x|+|y|$
If the last one can be replaced by a stronger condition
- $|x+y|\leq \max\{|x|,|y|\}$
then we say it is a non-Archimedean absolute value, otherwise it is Archimedean.
But when we generalize this concept, we have only the non-Archimedean requirement:
Here $\Gamma$ is a totally ordered abelian group with group operation written as multiplication.
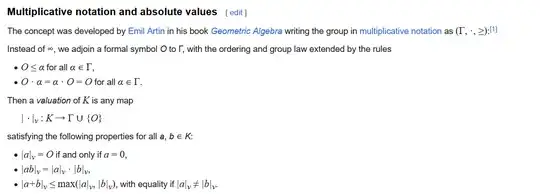
My problem is, what is the motivation of abandaoning the Archimedean version? Did that path exist in the history? Is the structure theorem of that generalization too trivial to be written?
Update: I found a literature that mentioned this set up: normed ring/field,
in A.G. Kurosh, "Lectures in general algebra" , Chelsea (1963) (Translated from Russian), and likewise we have Archimedean/non-Archimedean normed ring/field. But there is no any deep result with this definition.
