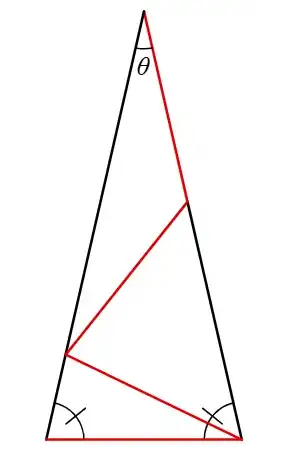
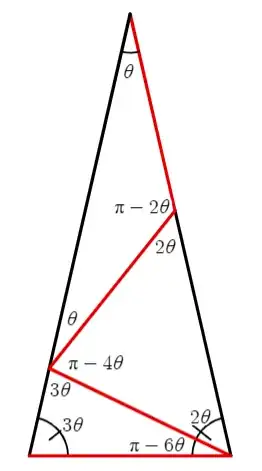
Is there a question that contains no numbers except $1$, whose answer is $\pi/7$?

Question

Is there a question that contains no numbers, except possibly $1$, whose answer is $\pi/7$ ?

There are plenty of questions with no numbers except $1$, whose answer is $\pi/n$ for small integer values of $n$ other than $7$. For some reason, $\pi/7$ seems to be unattainable.

Examples:

1. Evaluate $\int_{-\infty}^\infty \frac{\sin{x}}{x}dx$. Answer: $\color{red}{\pi}$

2. Drop a needle of length $1$ onto a floor with equally spaced parallel lines a distance $1$ apart. On average, how many times do you have to drop the needle until it crosses one of the lines? Answer: $\color{red}{\pi/2}$

3. What is the volume of a cone with unit base radius and unit height? Answer: $\color{red}{\pi/3}$

4. A regular $n$-gon of side length $1$ encloses a regular $(n+1)$-gon. The polygons are concentric, and for each $n$ the area of the inside polygon is maximized. What is the limit, as $n\to\infty$, of the difference in their areas? Answer: $\color{red}{\pi/4}$

5. On a sphere of diameter $1$, uniformly random points are chosen until there is a unique circle that passes through them. What is expected area of this (planar) circle? Answer: $\color{red}{\pi/5}$

6. A regular $n$-gon of side length $1$ is inscribed in a circle. What is the limit, as $n\to\infty$, of the difference between their areas? Answer: $\color{red}{\pi/6}$

7. $\color{red}{???}$

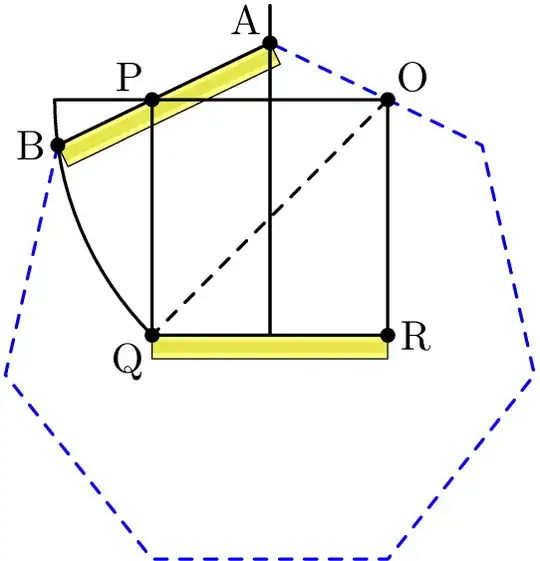
8. Like question 4, except the polygons do not have to be concentric. Answer: $\color{red}{\pi/8}$

Indirectly specifying a number is not allowed; for example, "heptagon" is equivalent to "$7$-gon" and is thus not allowed. The question should not be obviously ad hoc. (For example: "A unit circle is divided into $k$ equal parts, where $k$ is the product of the first even prime and the first odd prime, plus $1$. What is the area of each part?") I hope the spirit of my question is understood.

Answer 1

Given that the red line segments are congruent, find the value of $\theta$ in radians.

The answer is $\pi/7$.

Proof. Angle chasing gives the following angles:

Equating the equal angles of the largest isosceles triangle gives $3\theta=\pi-6\theta+2\theta$, which gives $\theta=\pi/7$.

---

This question was inspired by a similar question, whose answer is $\pi/9$.

Answer 2

You hinted at an answer in a comment:

A circle of radius $1$ is partitioned into sectors by radial lines, all of these sectors having equal area. What is the area of the largest such sector that cannot be constructed by compass and straightedge?

Answer 3

Question :
The Unit Circle is Dissected into $C$ Smaller Circles of Equal Size.
The $C$ Smaller Circles are arranged on the Euclidean Plane such that every Circle is Either touching every other Circle Or can reach every other Circle with a Single Circle in-between.
In other words , Every Circle is neighbours with every other Circle or it has a Common neighbour with the non-neighbouring Circles.
Every Pair of Circles will be made of neighbours or will have a Common neighbour.

What is the Minimum Area of those $C$ Smaller Circles ?

---

Dissection may not be the appropriate word. I will restate with other words :
The Unit Circle is covered with White Paint. Paints in various other colours will be given to colour a Set of Smaller Circles such that the total Paint Quantity is Equal to the White Paint Quantity , which is naturally $\pi$ Units.
The Smaller Circles are required to be arranged such that every Pair $(C_n,C_m)$ have a Common neighbouring Circle or are neighbours themselves.

What is the Minimum Paint Quantity of each colour ?

---

Answer :
$\pi/7$

---

Elaboration :
Basically Unit Circle Area = $\pi$ , Each Smaller Circle has Area $\pi/C$.

With $C=2,3,4,5$ , we have :

With $C=6$ , this will not work :

The 2 Purple Circles are not neighbours & have no Common neighbours.

With $C=6$ , this will work :

With $C=7$ , this will not work :

Here , the Purple Circle is too far from the Grey Circles.

Maximum $C$ is 7. We can arrange these Circles like this :

Every Circle is neighbours with every other Circle Or Every Circle is neighbours with the Centre Circle which is the Common Neighbour with the non-neighbouring Circles.
We can not have larger $C$.
Hence , Minimum Area of those $C$ Smaller Circles is $\pi/C=\pi/7$.
This is the Minimum Paint Quantity of each colour.

---

With $C=8$ , there is no way.

Here , the Grey Circle is too far from the Purple Circles.

Answer 4

A curious construction leading to $\pi/7$

In the following construction, circles of the same color are congruent.

Start with three red circles and a green circle inscribed in an angle $\theta$, as shown.

Then inscribe another green circle as high as possible, followed by two more red circles as high as possible. Perform this algorithm twice.

Then complete the triangle by drawing a horizontal line as high as possible, enclosing all the circles. Adjust $\theta$ so that the lowest three circles are all tangent to the base of the triangle.

Question:

What is $\theta$?

The answer is $\pi/7$.

---

Proof

Here is a calculation-free proof:

Draw a green circle surrounded by, and tangent to, seven equally spaced red circles. Choose the radius of the red circles so that a line can be tangent to the green circle, and the first and fourth red circles going say anticlockwise. Call this arrangement of circles a "heptaflower".



Draw two heptaflowers that share two neighboring red circles.



Add another heptaflower that shares two (non-neighboring) red circles with the previous lower heptaflower, as shown.



Then, based on the angles in a regular heptagon, we can draw lines tangent to the circles to form a triangle, exactly matching the tangencies in the question.



It follows that $\theta=\pi/7$.

To be sure, we should show that there can be only one value of $\theta$. This can be done using a proof by contradiction, as explained at the end of this answer to a similar question.

---

Generalization

In the construction above, the "algorithm" (adding another green circle and two more red circles) was performed twice, leading to seven red circles and $\theta=\pi/7$.

Performing it once leads to five red circles and $\theta=\pi/5$:

Performing it three times leads to nine red circles and $\theta=\pi/9=20^\circ$ (in the algorithm, circles of the same color are allowed to overlap):

(This reveals another property of the infamous 80-80-20 triangle.)

Answer 5

Here's a non-answer (as it requires a reference to $7$) that I nevertheless like.

Let $I_0$ be a segment of length $1$, and let $I_1$ be a semicircle sharing, say, endpoint $P$ with $I_0$. Thereafter, let $I_{n+1}$ be the involute of $I_n$ "emanating" from $P$.

As it happens, $$|I_n| = \frac{\pi^n}{n!}$$ Consequently, $$\frac{|I_n|}{|I_{n-1}|}=\frac{\pi}{n}$$ This (non-)answers OP's question for general $n$, as well as the particular $n=7$.

(I like to think that using $n$ to count iterations is somewhat less of a cheat than, say, dividing a unit circle into $n$ equal pieces.)

---

The figure is a special case $(\theta=\pi)$ of Y. S. Chaikovsky's construction of $\theta^n/n!$ (as described in this answer of mine and this entry on my Trigonography site and this article by Leo Gurin in The American Mathematical Monthly), which gives a visual representation of the power series of sine and cosine.

Above, taking the origin to be the center of the semi-circle, the power series connection is evident in the convergence of the resulting "polygonal spiral" to the point $(-1,0) = (\cos\pi,\sin\pi)$. The individual coordinates are the limits of the alternating sums of $|I_{even}|$ and $|I_{odd}|$, because the lengths of the involutes are —by the nature of involutes— also the lengths of the segments in the spiral.

Answer 6

Vietè's neusis construction of the regular heptagon:

Source file Licensing

Geometric details: OPQR is a unit square. The arc centred on O through Q is drawn, as is the perpendicular bisector of OP. The en:Neusis construction involves finding unit interval AB through P with A on the perpendicular bisector and B on the arc. Angle PAO is the interior angle of a heptagon. The remainder of the construction can be carried out with ruler and compass. (Two of the vertices lie on the lines OR and PQ.)