5

How do you calculate pitch & yaw for a camera so that it faces a certain 3D point?

Variables

  • Camera X, Y, Z
  • Point X, Y, Z

Current Half Solution

Currently I know how to calculate the pitch, and I do that using the following.

$dx:=camera_x-point_x$

$dy:=camera_y-point_y$

$dz:=camera_z-point_z$

$pitch:=atan2(\sqrt{dz*dz+dx*dx},dy))$

Then if $(dy>0)$ pitch gets negated. ($pitch:=-pitch$)

The Main Question

So how would I go about calculating the yaw?

Edit

This is the orientation of my axis.

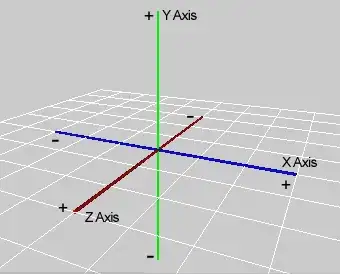
Orientation
(source: wikispaces.com)

Answer - Thanks to Omnomnomnom

$dx:=camera_x-point_x$

$dy:=camera_y-point_y$

$dz:=camera_z-point_z$

$pitch:=-atan2(dy, \sqrt{dx*dx+dz*dz})$

$yaw:=atan2(dz,dx)-90^\circ$

Community
  • 1
vallentin
  • 207

1 Answers1

7

So, we're going to describe camera direction needed to direct the camera positioned at $(0,0,0)$ at an $(x,y,z)$ point using the angles from spherical coordinates. The two angles are $\theta$ and $\phi$.

$\theta$, the azimuthal angle, normally taken from $0˚$ to $360˚$, is the angle made in the $xy$ plane between the $x$-axis and the line connecting $(0,0,0)$ to $(x,y,0)$. Simply put, this gives us our "yaw".

$\phi$, the polar angle, normally taken from $0˚$ to $180˚$, is the angle made between the $z$-axis and the line connecting $(0,0,0)$ to $(x,y,z)$. This gives us something like the pitch. That is, $\phi=90˚$ means that you're looking horizontally, whereas $\phi=0˚$ means that you're looking vertically upward.

Now, for a given point $(x,y,z)$, the calculations are as follows: $$ \theta = \arctan\left(\frac yx\right)\\ \phi = \arctan\left(\frac {\sqrt{x^2+y^2}}z\right) $$ So for example: to point your camera at the point $(1,1,1)$, you would need the angles $$ \theta = \arctan\left(\frac 11\right)=45˚\\ \phi = \arctan\left(\frac {\sqrt{2}}1\right) \approx 55˚ $$

Ben Grossmann
  • 234,171
  • 12
  • 184
  • 355
  • The x, y, z, what are they? are they the camera x, y, z or the target x, y, z or what? – vallentin Aug 18 '13 at 01:41
  • Sorry, the camera's coordinates are taken to be $(0,0,0)$, and the target's coordinates are $(x,y,z)$. If you're given a camera point and a target point, you could subtract the camera point from both to make this work. – Ben Grossmann Aug 18 '13 at 01:43
  • To put this in the language of your question: given a (dx,dy,dz), we calculate $$\theta=\operatorname{atan2}(dy,dx)\ \phi = \tan(\sqrt{dx^2+dy^2},z)$$ – Ben Grossmann Aug 18 '13 at 01:49
  • Well that didn't work, the camera is completely facing away and rotating weirdly no matter how I mode it around. When I move the camera up and down [Y] then camera faces down and up correctly though it also rotates left and right. When I move the camera in either X and/or Z then camera makes all kinds of weird turns. – vallentin Aug 18 '13 at 01:50
  • Well, what we have here is a miscommunication. For me, the horizontal axes are $x$ east-west, $y$ north-south, and $z$ up-down. What are x,y, and z for you? – Ben Grossmann Aug 18 '13 at 01:52
  • Look at edited post, I added a picture of the axis I'm using. – vallentin Aug 18 '13 at 01:55
  • 1
    Okay, in this case, your clockwise yaw ($0˚$ in direction of $x$-axis, increasing the angle moves you clockwise from above in the $xz$ plane) is given by $$a_1=\operatorname{atan2}(dz,dx)$$ you pitch, as in the angle that your direction makes with the $xz$ horizontal, is given by $$a_2 = \operatorname{atan}(dy,\sqrt{dx^2+dz^2})$$ This gives you an angle of $0˚$ when looking horizontally, and $90˚$ when looking along the $y$-axis. – Ben Grossmann Aug 18 '13 at 02:01
  • Thanks a bunch, that did the trick! I added the final solution to my post also. – vallentin Aug 18 '13 at 02:11
  • Glad you got it working. I realize, after reviewing your post again, that I had my dx,dy, and dz backwards. I was taking (point coordinate) - (camera coordinate) instead of the other way around, which necessitated your fudging with my answer a bit. – Ben Grossmann Aug 18 '13 at 02:16
  • Well that's okay, in the end everything worked out! And as you can see in my post I did change some things about the calculations, so yea I played with it to get it to work. – vallentin Aug 18 '13 at 02:20