How do I reparametrize thresholded Generalized Logistic function to have a parameter for $x$ intercept?

Question

This is the equation of Generalized Logistic function

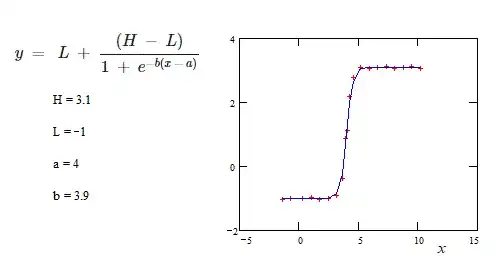
$$y\ =\ \ L\ +\ \frac{\left(H\ -\ L\right)}{C\ +\ Qe^{-b\left(x\ -\ a\right)}}$$

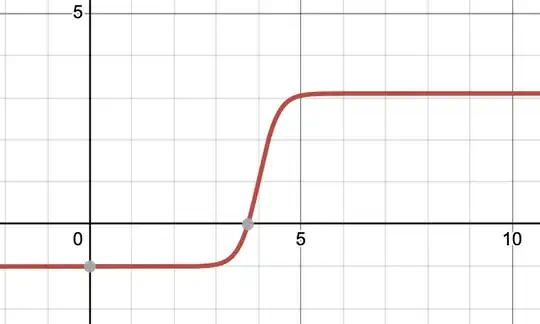
which looks like this:

For $L < 0$, I can take the $\max$ of this function with $0$ to get

$$y = \max (0, \ \ L\ +\ \frac{\left(H\ -\ L\right)}{C\ +\ Qe^{-b\left(x\ -\ a\right)}}) \ldots (1)$$

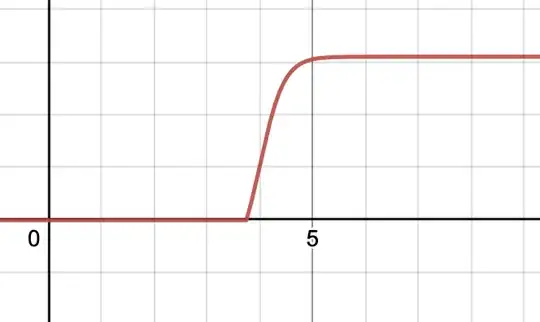
which looks like this:

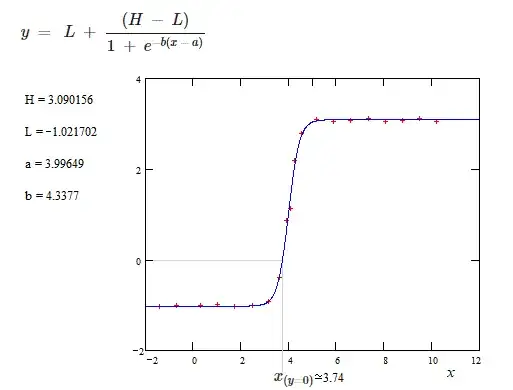
This function always intersects the $x$-axis when $L < 0$, and the intercept is the solution of $\ \ L\ +\ \frac{\left(H\ -\ L\right)}{C\ +\ Qe^{-b\left(x\ -\ a\right)}} = 0$ when we solve for $x$

I want to re-parametrize $(1)$, so that the equation contains a parameter for this intercept like we have in the equation of line $y = b(x-a)$ where $a$ is the $x$ axis intercept.

Is there a clean way to achieve this?

Solving $\ \ L\ +\ \frac{\left(H\ -\ L\right)}{C\ +\ Qe^{-b\left(x\ -\ a\right)}} = 0$ for $x$ gives $x = a - \frac{1}b \cdot \ln \left(\frac{1 - (H/L) - C}{Q}\right)$ which already starts to look messy.

The goal is to use $(1)$ to fit to my data and easily retrieve the $x$ intercept posterior samples using Bayesian methods.

Answer 1

$$y\ =\ \ L\ +\ \frac{\left(H\ -\ L\right)}{C\ +\ Qe^{-b\left(x\ -\ a\right)}}$$ They are too many parameters in your formula.

I suppose that the limits for $x\to\pm\infty$ are $H$ and $L$. This implies $C=Q=1$.

In fact this is the four parameters logistic equation : $$y\ =\ \ L\ +\ \frac{\left(H\ -\ L\right)}{1\ +\ e^{-b\left(x\ -\ a\right)}}$$

By inspection only one can roughly evaluate the parameters $H,L,a,b$ :

$H\simeq 3.1$ .

$L\simeq -1$ .

$a\simeq 4\quad$ Abscissa of the middle point $(x\simeq 4\:,\: y\simeq 1)$ .

$b\simeq 3.9\quad$ from the slope at middle point $y'(a)=p\simeq 4$ (graphically measured). $$y'(x)\ =b\ \frac{\left(H\ -\ L\right)}{(1\ +\ e^{-b\left(x\ -\ a\right)})^2}\quad\implies\quad p=y'(a)\ =b\ \frac{\left(H\ -\ L\right)}{(2)^2}$$ $$b=\frac{4p}{H-L}\simeq \frac{16}{4.1}$$

$x_{(y=0)}=a+\frac{1}{b}\ln(-L/H)\simeq 3.71$

For better fitting one need non-linear regression (result below) :

$x_{(y=0)}=a+\frac{1}{b}\ln(-L/H)\simeq 3.74$

The main discrepancy is for $b$. This is due to the low accuracy of the graphical evaluation of the slope by inspection method.