3

My friend asked me if I could help her with a few problems, and they are mostly quadratics of trig functions and easy manipulations. But I was surprised to find equations such as $5 \sin (2x)=1$ and $10\sin(x-2)=-7$ because to me it seems you need to use inverse trig functions to solve this. The problem is, the problem set with inverse trig functions only starts later. Is there a way to solve these without explicitly using inverse trig functions? Thanks.

Soham
  • 10,120
Ovi
  • 24,817
  • 2
    $$5\sin 2x=1\implies x=\frac12\arcsin\frac15$$ – DonAntonio Aug 17 '13 at 21:10
  • 4
    @DonAntonio: I think the question is if this can be done without a calculator and inverse trig functions. – Thomas Aug 17 '13 at 21:12
  • 1
    Well, that is not the question but I agree, @Thomas, that that was very probably the intention. Yet without learning by heart the sine/cosine/tangent tables, as some russian colleagues used to do (!!), I can't see any way out of this... – DonAntonio Aug 17 '13 at 21:13
  • 2
    @DonAntonio The question says "Is there a way to solve these without explicitly using inverse trig functions?" – Fly by Night Aug 17 '13 at 21:59
  • Probably the moral is: The friend should as her instructor for help, and not us (since we do not know what was intended, and cannot guess). – GEdgar Aug 18 '13 at 00:10

3 Answers3

3

From this answer: https://math.stackexchange.com/a/87768/26188 you get that $\sin(x)$ is never $\frac{1}{5}$ when $x$ is of the form $\frac{p\pi}{q}$ for any integers $p$ and $q$. So finding an exact solution to $5\sin(2x) = 1$ might be too much to ask of someone in pre-calculus. You have likewise for your second equation.

Community
  • 1
Thomas
  • 44,491
2

$\sin (2x) = 0.2$

Applying double angle formula, we have $2 \sin x \cos x = 0.2$

$\sin (x) \sqrt{1 – \sin^2{x}} = 0.1$

$\sin^2 (x) \left( 1 – \sin^2 x \right) = 0.01$

$\ -sin^4x + \sin^2x – 0.01 = 0$, which is now quadratic in $\sin^2x$.

Note 1. Normally this question should not be solved this way.

Note 2. Squaring will produce unnecessary roots.

Note 3. However, you still need the inverse of sine to find what x is.

Note 4. Course started on trigonometric identities?

Note 5. Double angle formula starts even later in the course.

Mick
  • 17,431
  • She did not just start the course, she already finished but she was doing a summer assigment before a calculus course – Ovi Aug 18 '13 at 17:44
  • Gd. Then she shouldn't have any problem in understanding the above. – Mick Aug 19 '13 at 04:07
  • Well yea it just bothered me that the section titled "inverse trigonometric functions" was later in the packet. – Ovi Aug 19 '13 at 14:51
1

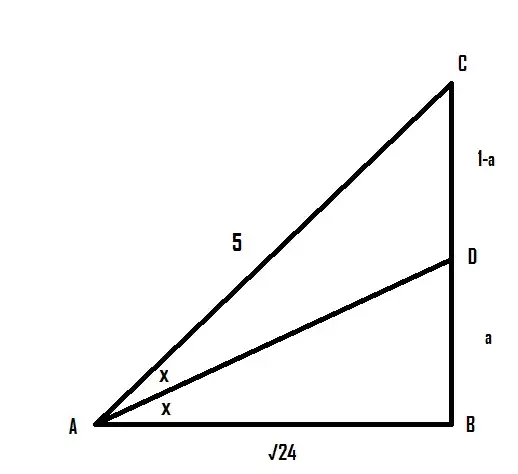enter image description here$5 \sin (2x)=1 \Rightarrow \sin(2x)=\frac{1}{5}=\frac{opposite side}{hypoteneous}$

$\frac{CD}{DB}=\frac{AC}{AB} \Rightarrow \frac{1-a}{a}=\frac{5}{\sqrt(24)} \Rightarrow a=\frac{ \sqrt(24)}{5+ \sqrt(24)} \Rightarrow AD=\sqrt(24) \frac{\sqrt(1+(5+\sqrt(24))^2)}{5+\sqrt(24)} \Rightarrow \sin(x)=\frac{1}{\sqrt(1+(5+\sqrt24)^2)}$

Since $a$ is very small $\Rightarrow x$ is very small and for small angles $\sin x \approx x$

$\therefore x=\frac{1}{\sqrt(1+(5+\sqrt24)^2)} \approx 0.1$

Vikram
  • 5,808
  • Perhaps you should write that $\sqrt{24} \approx 5$ so that the final expression can be reduced by hand (in particular, without a calculator). – Bilbottom Aug 26 '18 at 15:11
  • @Vikram How do you know that $\frac{CD}{DB} = \frac{AC}{AB}$? – Toby Mak Oct 18 '18 at 12:24