Consider the system $$\begin{cases}\dot{x}=x+y\cos(y)\\ \dot{y}=-y \end{cases}$$ which has the unique equilibrium point $(0,0)$. I want to find the invariant manifolds for this system. The Jacobian at the origin is $$\begin{pmatrix} 1&1\\ 0&-1 \end{pmatrix}$$ which has eigenvalues $\lambda_1=1$ and $\lambda_2=-1$. An eigenvector for $\lambda_1$ is $v_1=(1,0)^\intercal$ and for $\lambda_2$, an eigenvector is $v_2=(1,-2)^\intercal$. It is clear that the unstable manifold is the unstable subspace $\operatorname{span}(v_1)$ aka the $x$-axis. However, I am completely lost on how to find the stable manifold. How does one go about finding this?
Asked
Active
Viewed 304 times
1 Answers
5
You can solve for the trajectories directly. Observe, \begin{align} \frac{dx}{dy} &= \frac{\dot{x}}{\dot{y}}\\ &= \frac{x + y\cos(y)}{-y} \end{align} By Mathematica, this has the general solution \begin{align} x &= \frac{C - \cos(y)}{y} - \sin(y) \,,\quad C \in \mathbb{R} \end{align} We need $\lim_{y \to 0} x(y) = 0$, so we infer that $C = 1$. Thus, we have the equation for the unstable manifold: \begin{align} \boxed{x = \frac{1 - \cos(y)}{y} - \sin(y) } \end{align}
To verify that this is the case, we can view a plot of the phase portrait:
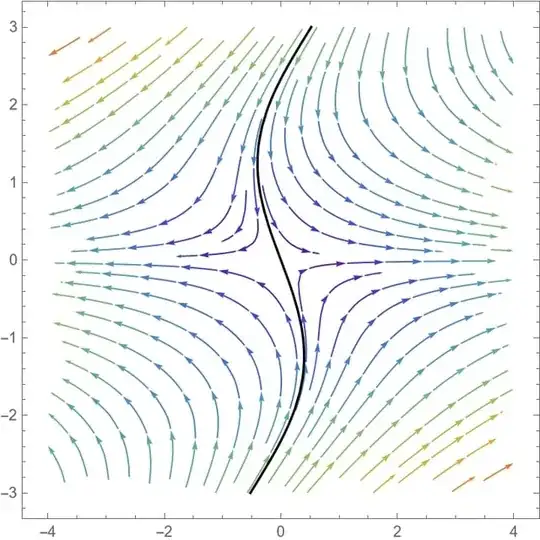
If you want to play around with this, here's some Mathematica code:
sol = DSolve[{x'[y] == (x[y] + y*Cos[y])/-y, x[0] == 0}, x[y],
y][[1]] // FullSimplify
xmin = -4; xmax = 4; ymin = -3; ymax = 3;
cplot = ContourPlot[
x == (x[y] /. sol), {x, xmin, xmax}, {y, ymin, ymax},
ContourStyle -> {Black}];
splot = StreamPlot[{x + y*Cos[y], -y}, {x, xmin, xmax}, {y, ymin,
ymax}, StreamColorFunction -> "Rainbow"];
Manipulate[
Show[splot, cplot,
ParametricPlot[
Evaluate[
First[{x[t], y[t]} /.
NDSolve[{x'[t] == x[t] + y[t]*Cos[y[t]], y'[t] == -y[t],
Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0,
T}, PlotStyle -> Red]], {{T, 20}, 1, 100}, {{point, {3, 0}},
Locator}, SaveDefinitions -> True]
AlkaKadri
- 2,270