7

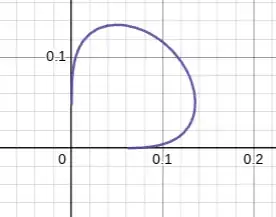
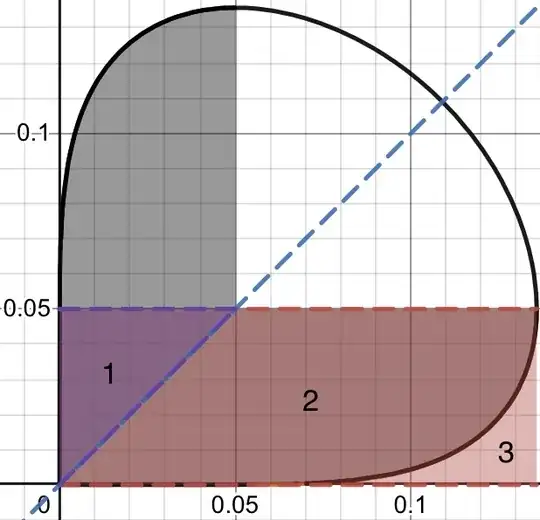
Finding the area surrounded by the part of the implicit equation $\sin (y^x) = \cos (x^y)$ such that $y\le 2n-x$ where $n$ is the solution to $n^n=\frac{\pi}{4}$ where $n<0.5$ bounded by the $x$ and $y$ axes.

This problem has no context because I am trying to solve it just for fun.

First, I knew what part of the implicit equation I wanted to find the area of (the part that looks similar to a lemniscate) but I did not know how to properly define the integral because I realized I could not find the bounds of this part of the equation easily.

I then manipulated the equation $\sin (y^x) = \cos (x^y)$ into $y^x = \sin^{-1}(\cos (x^y))$ which I then realized I could simplify it to $y^{x}+x^{y}=\frac{\pi}{2}$.

I am currently struggling to find the bounds to set up the integral which I will then hopefully be able use to find the area. I have tried using the implicit derivative but to no avail.

My only success so far was to find the point where the slope is $-1$ which is $(n,n)$ where $n$ is the solution to $n^n=\frac{\pi}{4}$ where $n<0.5$ although I am not sure if this information is actually helpful.

Here is my graph on Desmos if anyone wants to see it: https://www.desmos.com/calculator/x3lfyatuxj

Thanks for the help in advance

Edit: While randomly trying things in the calculator, I found that the equation $y=ex$ goes through the local maximum.

I can plug this in to the original equation to get $x^{ex}+e^{x}x^{x}=\frac{\pi}{2}$.

I thought I would be able to easily find x but I was unable to and WolframAlpha just gave the approximation of $x\approx0.0499491320167935$. It also gives a solution of $x\approx0.508081340341750$ but it is outside of the original bounds $y\le 2n-x$.

Dylan Levine
  • 2,122
  • 3
    if $y=0$, you get $0+1=\pi/2$ – MathFail May 10 '23 at 02:23
  • The problem is not just evaluating the maximum bounds. Can you tell the limit of the function(s) at $(0, 0)$. Can this be included in the integral? Considering $\pi/2$ is a transcendental value, it is very difficult to setup a parametrization for $x, y$ in terms of another variable, $t$ . – Dstarred May 10 '23 at 03:38
  • Furthermore, your initial simplification is wrong: $$\sin^{-1}{\left(\sin{y^x}\right)} = \sin^{-1}{\left(\sin{(x^y + \pi/2)}\right)} \ \Leftrightarrow y^x = x^y + \pi/2 \ \Leftrightarrow y^x - x^y = \pi/2$$. This is also restricted under the domain that $-\pi/2 \le y^x \le \pi/2$ and $-\pi/2 \le x^y + \pi/2 \le \pi/2$. – Dstarred May 10 '23 at 03:42
  • @Dstarred I am pretty sure the portion of the function I am looking at is restricted under that domain.

    Also, how should I go about solving this problem?

     – Dylan Levine May 10 '23 at 11:15
  • Can I define the original function as $\sin y^x = \cos x^y$ such that $y\le 2n-x$ where $n$ is the solution to $n^n=\frac{\pi}{4}$ where $n<0.5$ – Dylan Levine May 10 '23 at 11:22
  • Thanks for the help @TymaGaidash. I looked into those ideas a little but I will try them out more seriously now. I also updated the question. – Dylan Levine May 10 '23 at 13:10
  • If you are not setting any boundaries on x and y besides x,y>0, I'd advise you not to try to solve this problem. Here's a more accurate plot of the function: sin^=cos^ – Carlos May 10 '23 at 03:21
  • 1
    @TymaGaidash I am looking for an exact expression or steps toward finding an exact expression. – Dylan Levine Aug 12 '23 at 19:59
  • It looks like a guitar pick. Monte Carlo approximation in $x,y \in [0,0.14]$ box gives area close to 0.01525119... I also suggest actual geometric integration for an exact answer – vallev Aug 14 '23 at 22:29
  • 2
    Note that it is wrong that $\sin(y^x)=\cos(x^y)\iff y^x+x^y=\pi/2$. We have $\sin(y^x)=\cos(x^y)$$\iff \sin(y^x)=\sin(\pi/2-x^y)$$\iff \sin (y^x)-\sin(\pi/2-x^y)=0$$\iff 2\cos\frac{y^x+\pi/2-x^y}{2}\sin\frac{y^x-\pi/2+x^y}{2}=0$$\iff \frac{y^x+\pi/2-x^y}{2}=\pi/2+s\pi$ or $\frac{y^x-\pi/2+x^y}{2}=t\pi\iff y^x-x^y=\pi/2+2s\pi$ or $y^x+x^y=\pi/2+2t\pi$ where $s,t\in\mathbb Z$. – mathlove Aug 15 '23 at 04:42
  • Why have the answer accepted for this long? – Тyma Gaidash Oct 14 '24 at 16:43
  • @ТymaGaidash I was looking through some of my older questions and realized that it was a partial answer so I un-accepted it. I must have forgot before – Dylan Levine Oct 14 '24 at 21:31
  • "I am pretty sure the portion of the function I am looking at is restricted under that domain." As far a I see, you have $x,y>0$, so both $x^y$ and $y^x$ are positive and so not $x^y+\pi/2\le \pi/2$. – Alex Ravsky Nov 25 '24 at 08:31
  • The solution of $n^n=\frac \pi 4$ is given in terms of Lambert function $$n=\frac{\log \left(\frac{\pi }{4}\right)}{W_{-1}\left(\log \left(\frac{\pi }{4}\right)\right)}$$ – Claude Leibovici Nov 29 '24 at 10:31
  • 1
    This question now lives on https://mathoverflow.net/questions/485382/ – Fred Hucht Jan 20 '25 at 09:35

1 Answers1

11

$\def\E{\operatorname E}$ Partial answer

Applying Lagrange reversion, a Stirling S2 $s_n^{(m)}$ differentiation formula, and factorial power $n^{(m)}$:

$$x^y+y^x=\frac\pi2\implies y=\sum_{n=1}^\infty\frac1{n!}\left.\frac{d^{n-1}}{dy^{n-1}}\left(\frac\pi2-x^y\right)^\frac nx\right|_0=\sum_{n=1}^\infty\sum_{k=0}^n\left(\frac nx\right)^{(k)}\frac{s_{n-1}^{(k)}(-1)^k}{n!}\left(\frac\pi2-1\right)^{\frac nx-k} \ln^{n-1}(x)$$

but this is hard to integrate, so we expand. Each sum can go to $\infty$ and, numerically, can be switched. Next, convert to the Pochhammer symbol $(n)_m$, $a^{(k)}=(a-k+1)_k$, and use its Stirling S1 $S_n^{(m)}$ expansion. Also, we switch sums to apply $\frac{d^nx^m}{dm^n}=x^m\ln^n(x)$:

$$x^y+y^x=\frac\pi2\implies y=\sum_{m=0}^\infty\sum_{n=1}^\infty\sum_{k=0}^n(-1)^{k+n+1}n^m\frac{S_k^{(m)}s_{n-1}^{(k)}}{n!}\left(\frac\pi2-1\right)^{\frac nx-k}\frac{d^{n-1}}{dm^{n-1}}x^{-m}$$

shown here. $y(x)$ is the branch bounding region $2$.

The actual maximum of $x^y+y^x=\frac\pi2$ is where $\frac d{dx}\left(x^y+y^x-\frac\pi2\right)=0\iff yx^y+xy^x\ln(y)=0$ intersects it at $(a,b)=(0.0500360\ldots,0.1357758\ldots)$. The Lagrange reversion series requires increasingly more terms as $x\to a$ for accuracy, but does not diverge, so it is plausible to assume the series works on the entire branch. Therefore, region $3$’s area uses the En function:

$$\begin{aligned}\int_0^a y(x)dx=\int_0^b \sum_{m=0}^\infty\sum_{n=1}^\infty\sum_{k=0}^n(-1)^{k+n+1}n^m\frac{S_k^{(m)}s_{n-1}^{(k)}}{n!}\left(\frac\pi2-1\right)^{\frac nx-k}\frac{d^{n-1}}{dm^{n-1}}x^{-m} dx=\sum_{m=0}^\infty\sum_{n=1}^\infty\sum_{k=0}^nS_k^{(m)}s_{n-1}^{(k)} (-1)^{k+n+1}\frac{n^m}{n!}\left(\frac\pi 2-1\right)^{-k}\frac{d^{n-1}}{dm^{n-1}}\left(b^{1-m}\E_{2-m}\left(-\frac nb\ln\left(\frac\pi2-1\right)\right)\right)\end{aligned}$$

which is supported by the two expressions being equal; much more computation is needed for more terms in the linked series, so we approximate the area using the integral of the series. Region $1,2,3$ add to $ab$, so region $2$’s area is $ab$ minus region $1$’s and $3$’s areas.

Therefore the shaded area should be:

$$\boxed{2ab-a^2-2\sum_{m=0}^\infty\sum_{n=1}^\infty\sum_{k=0}^nS_k^{(m)}s_{n-1}^{(k)} (-1)^{k+n+1}\frac{n^m}{n!}\left(\frac\pi 2-1\right)^{-k}\frac{d^{n-1}}{dm^{n-1}}\left(b^{1-m}\E_{2-m}\left(-\frac nb\ln\left(\frac\pi2-1\right)\right)\right)\approx0.00985}$$

For the rest of the area, we need a series or parametrization for the curve’s other branch. Although an approximation would be simpler, this is an exact answer.

Тyma Gaidash
  • 13,576