Finding circle tangent to a line and intersecting a given point

Question

Background

I am trying to understand a historical engineering drawing intended for machinists producing a part. I am neither an engineer, nor a machinist, and have only a basic understanding of such drawings. As is apparently typical for such drawings, they contain measurements related to different datum positions on the part itself, with those datum positions measured relative to an origin point. This generally makes it easy to understand the part's various dimensions. However, there is a section of the drawing that confuses me, which I will describe below.

Additionally, it has been many years since I have needed to do more than the most basic geometry and so my knowledge is quite rusty.

I have looked at several other questions/answers both here and elsewhere, but not yet found an approach that works for me (or if I have, I haven't recognized it). I have also made a simple computer program of the problem restated slightly differently (e.g. while constraining Point C to lie on a circle of radius r from Point A, I can iteratively move the x and y coordinates of Point C until Point B is close to intersecting the line, but it's not exact) but am unsure how to find a more analytical solution. I appreciate your patience and help.

Description

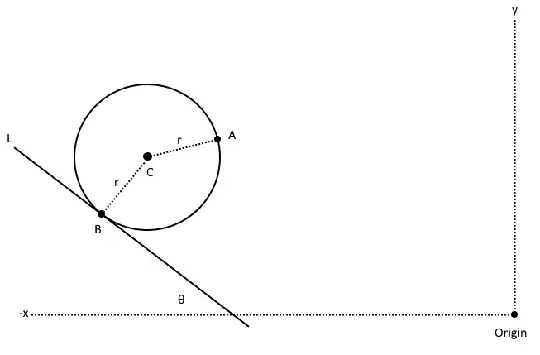
This section of the part has a Line L of known slope and y-intercept. The position (in the x-y coordinate system in the drawing) of Point A is known. Line L and Point A are connected by a concave-up circular arc of known radius r.

The drawing does not specify the center of the circle (Point C), nor the coordinates of the single point that the circle intersects Line L (Point B). Thus, while it's known that Point A lies on the circle, since Points B and C are unknown it then it is also unknown where on the circle Point A lies.

Question

Given the coordinates of Point A, the radius r of the circle, and the equation of Line L, what are the coordinates of Point B where Line L intersects the circle?

Thank you.

Other Information

Known:

• x and y coordinates for Point A.
• Equation (i.e. slope [theta] and y-intercept) for Line L.
• Radius r of the circle.
• Fact that Line L is tangent to the circle, and that Point B is the point of tangency.
• Fact that no point, line, etc. lies on or intersects the origin.
• Fact that all portions of this part lie in the -x and +y quadrant, relative to the origin.

Unknown:

• Angle ACB
• x and y coordinates of Point B, the point of tangency.
• x and y coordinates for Point C, the center of the circle.

Desired Quantities:

• x and y coordinates of Point B, the point of tangency.
• x and y coordinates of Point C, the center of the circle.

Answer 1

We can proceed according to the following sketch as follows:

1. Consider the equation for the line $L'$ parallel to line $L$: $y=mx+q$, then we have for line $L'$:

$$y=mx+q+\frac{r}{\cos \theta}$$

2. Consider the equation for the circles with center $C=(x_C,y_C)$ on the line $L'$ ($x_C$ is free):

$$\left(x-x_C\right)^2+\left(y-mx_C-q-\frac{r}{\cos \theta}\right)^2=r^2$$

3. Use the condition that circle contains $A=(x_A,y_A)$

$$\left(x_A-x_C\right)^2+\left(y_A-mx_C-q-\frac{r}{\cos \theta}\right)^2=r^2$$

which is a quadratic equation for $x_C$, we have indeed two solutions.

Finally we can find $y_C$ then the equation(s) for the circle(s) and then the coordinates for point(s) $B$.

Note: the assumption for a specific quadrant is not relevant for the solution.

---

Numerical example

Let consider the following givens:

• $L$: $y=-\frac{\sqrt 3}3x+10\frac{\sqrt 3}3$
• $\theta = 30°$
• $A=(4,3\sqrt 3)$
• $r=1$

Then we have:

1. Equation for the line $L'$:

$$y=-\frac{\sqrt 3}3x+4\sqrt 3$$

2. Consider the equation for the circles with center $C=(x_C,y_C)$ on the line $L'$ ($x_C$ is free):

$$\left(x-x_C\right)^2+\left(y+\frac{\sqrt 3}3x_C-4\sqrt 3\right)^2=1$$

3. Use the condition that circle contains $A=(4,3\sqrt 3)$

$$\left(4-x_C\right)^2+\left(3\sqrt 3+\frac{\sqrt 3}3x_C-4\sqrt 3\right)^2=1\iff 4x_C^2-30x_C+54=0$$

which leads to the following solutions:

• $x_C=3\implies y_C=3\sqrt 3, \;B=\left(\frac 5 2,\frac{5\sqrt 3}2\right)$

• $x_C=\frac 9 2\implies y_C=\frac{5\sqrt 3}2, \;B=\left(4,2\sqrt 3\right)$

Answer 2

I'm taking a step back, looking at the elementary geometry behind the problem. This is done by seeking a straightedge-compasses construction. Or, maybe, two.

Let $X$ be the center of the required circle*. (* -- Yes I'm playnig a little dumb here. We will eventually see that there isn't just "the" unique circle.) Then the radius $r$ must be the distance from $X$ to the given line $L$ and must also be the distance from $X$ to $A$.

Distance from $X$ to $L$

Construct a pair of perpendicular lines to $L$. Along these lines mark off the distance $r$ from the feet of the perpendiculars into the half-plane containing $A$. The points constructed in this way define a line $M$ parallel to $L$ and containing the required center.

Distance from $X$ to $A$

Construct the circle with radius $r$ centered on $A$. This circle contains the required center along with line $M$ rendered above, and so the intersection of the circle with $M$ will be the required center. It remains only to construct the circle centered on $X$ and passing through $A$. You will find that this circle is tangent to $L$ at $B$.

Double or Nothing

Well ... it becomes evident that the line and circle constructed above will fail to reach each other unless $r$ is greater than or equal to half the distance from $A$ to $L$. On the other hand, if $r$ is strictly greater than that distance then the constructed circle and line cut through each other and thus we find two points of intersection that may be defined as $X$. In general, then, you should expect two solutions when there are any to begin with.

Answer 3

Solution with vectors.

For the line $ax+by+c=0$, we can find the unit normal vector as $ \frac{<a,b>}{\sqrt{a^2 +b^2} }$, and a generic point on the line can be written as $< x, \frac{c-ax}{b} >$, we have the equation of points on a circle $\langle u , v \rangle$ as:

$$ | \langle x,\frac{c-ax}{b} \rangle \pm \frac{r}{\sqrt{a^2 +b^2 }} \langle a,b \rangle -\langle u,v \rangle | =r$$

To find the value of $x$, evaluate the coordinates $ \langle u , v \rangle $ at the coordinates of $A$. Done!

---

Note, you'd need to check the sign of the distance of the line to the additionally give point to write down the correct equation. See here for more info

Answer 4

I have one more solution. Let the coordinates of the centre be $(h,k)$ and so the equation of circle is $$(x-h)^2+(y-k)^2=r^2$$ Let's say that the coordinates of point $A$ is $(p,q)$ so we can say that $$(p-h)^2+(q-k)^2=r^2\tag{1}$$ Also since the line $L$ touches the circle $$\frac{|ah+bk+c|}{\sqrt{a^2+b^2}}=r\tag{2}$$ So from these two equations we can solve for $(h,k)$ and we can write the equation of circle. Now we have to just find the coordinates of point $B$.

So the equation of circle is $$x^2+y^2-2hx-2ky+h^2+k^2-r^2=0$$ Let the coordinates of point $B$ be $(r,s)$ so the equation of tangent at this point will be (the $T=0$ method) $$xr+ys-h(x+r)-k(y+s)+h^2+k^2-r^2=0$$ Now since this line is same as $ax+by+c=0$ the ratio of coefficients of $x$ and $y$ and the ratio constants must be same. So we can say that $$\frac{a}{r-h}=\frac{b}{s-k}=\frac{c}{h^2+k^2-r^2-hr-ks}\tag{3}$$ From this equation, you can find $(r,s)$ by comparing.

Answer 5

Let the coordinates of the point $B$ be $(h,k)$ then the equation of circle that touches the line $L$ at the point $B$ is given by $$(x-h)^2+(y-k)^2+\lambda(ax+by+c)=0$$ where $\lambda$ is a parameter and $a,b,c$ are known constants. Now this circle passes through the given point $A$ say $(p,q)$ so we can say that $$(p-h)^2+(q-k)^2+\lambda(ax+by+c)=0\tag{1}$$ also $$ha+kb+c=0\tag{2}$$ Now rearranging gives $$x^2+y^2-x(2h-\lambda a)-y(2k-\lambda b)+h^2+k^2+\lambda c=0$$ so the radius of circle is $$r=\sqrt{\left(\frac{2h-\lambda a}{2}\right)^2+\left(\frac{2k-\lambda b}{2}\right)^2-h^2-k^2-\lambda c}\tag{3}$$ Now we have three equations and three variables and so we can get the equation of circle. And then we can get coordinates of the point $B$. This solution is solely based on coordinate geometry.

Answer 6

Let the line by given by

$ y = m x + b $

The first step is to transform this implicit equation of the line into a parametric (explicit) vector equation, as follows:

From the above equation, the unit normal to the line is $N = \dfrac{(m , -1)}{\sqrt{1 + m^2}} $, so the direction vector is $d = \dfrac{(1, m)}{\sqrt{1 + m^2}} $. Also, let $P_0$ be any point on the line, for example, we can take $P_0 = (0, b) $.

The vector equation of the line is

$ P(t) = P_0 + t d $

Now, point $B$ is on the line, so

$ B = P_0 + t d $ for some $t \in \mathbb{R} $

Point $C$ is off by $r$ from point $B$, i.e.

$ C = B + r N $

We have to make sure here that $N$ is pointing in the right direction, and to check that we compute the quantity $ N \cdot (A - P_0) $. This should be positive; if it is not then simply negate the vector $N$, i.e. redefine $N$ as the negative of its initial value.

Now, we're set. We want the distance between $C$ and $A$ to be equal to $r$, hence by the distance formula,

$ r^2 = (C - A) \cdot (C - A) = (B + r N - A ) \cdot (B + r N - A) = (P_0 + t d + r N - A) \cdot (P_0 + t d + r N - A) $

Expanding the right hand side, and keeping in mind that $d$ and $N$ are unit vectors, and that $d$ is perpendicular to $N$, we obtain,

$ r^2 = (P_0 - A) \cdot (P_0 - A) + t^2 + r^2 + 2 t d \cdot (P_0 - A) + 2 r N \cdot (P_0 - A) $

Cancelling the $r^2$ term on both sides, gives us,

$ t^2 + 2 t d \cdot (P_0 - A) + 2 r N \cdot (P_0 - A) + (P_0 - A) \cdot (P_0 - A) = 0 $

Since $r$ is known and fixed, this a quadratic equation in $t$ that has two solutions (if $A$ is less than $2r$ away from line $L$).

Once we solve the quadratic equation by the quadratic formula, and get the two values of $t$, then for each value of $t$ we'll have a point $B$ and a corresponding point $C$.

Answer 7

Suppose that the radius of the circle, r, is NOT specified. We could ask for the locus of centers of the solution circles.

Then what we get is ...

(wait for it)

(scroll down more)

a parabola (because we are giving the equivalent of the locus definition)!

Note that this view clarifies the "two solutions" mentioned, that others found, one on either side of the axis of symmetry.