What are the necessary and sufficient conditions for the existence of a bang-bang controller in LTI systems? I think that a condition is that all the eigenvalues must have nonpositive real part. Are there more conditions? What about the multiplicity of the eigenvalues?
-
2stabilizing bang-bang controller? – Rollen S. D'Souza Apr 28 '23 at 16:23
-
You should ask this type of question on electronics SE even if it has a mathematical part... – Jean Marie Apr 28 '23 at 16:47
-
Yes, of course I want my controller to be a stabilizing one. – dodo Apr 29 '23 at 08:17
-
2@JeanMarie I disagree, this is a question about control theory, not about electronics. The LTI system in question is unspecified, hence could be arbitrary, even some kind of biological system. I also don't see the relevance of the linked question, as it is about a very practical aspect of bang-bang control, while this question is about control theory (ie existence conditions). – SampleTime Apr 29 '23 at 12:31
-
2@SampleTime You are right ; I have found for example an interesting answer here. – Jean Marie Apr 29 '23 at 12:39
-
@JeanMarie Thanks, that answer looks indeed very interesting! – SampleTime Apr 29 '23 at 12:41
-
@SampleTime you are very right sir. My textbook states that : if a LTI system is 1) fully controllable and 2) all the eigenvalues have non-positive real part, then exists a unique bang-bang solution such that I can bring any initial state to the origin in minimum time. Now, I would like to know more in the case of eigenvalues' multiplicity greater than one. – dodo Apr 29 '23 at 12:41
-
Considering that your question has the tag optimal-control, I assume that you consider so optimality condition under some input constraints (i.e. $|u|\leq1$), such as minimal time or $\min\int_0^T x^\top!(t),Q,x(t),dt$. Can you add the exact context for bang-bang control to your question? – Kwin van der Veen Apr 29 '23 at 13:07
-
Also the system from question JeanMarie links to is unstable, but still has a basin around the origin that can be driven to the origin using bang-bang control. So depending on $x(0)$ any controllable LTI system can be driven to the origin using bang-bang control. Considering your question I assume that you want existence of stabilizing bang-bang control $\forall x(0)\in\mathbb{R}^n$, is that correct? – Kwin van der Veen Apr 29 '23 at 13:14
-
@KwinvanderVeen yes, you got the point. With input costraints like $|u|\leq 1$, when does exist a stabilizing bang-bang for every initial condition? Do you have any reference? – dodo Apr 29 '23 at 13:31
1 Answers
Considering the following system
$$ \dot{x}(t) = A\,x(t) + B\,u(t), \tag{1} $$
with $x(t)\in\mathbb{R}^n$, $u(t)\in\mathbb{R}^m$, $A\in\mathbb{R}^{n\times n}$, $B\in\mathbb{R}^{n\times m}$, $x(0) = x_0\in\mathbb{R}^n$ and $u(t) \in \cal{U}$, where $\cal{U}$ is some convex set around containing the origin (for example $-1 \leq u_i(t) \leq 1\ \forall\ i\in\{1,\dots,m\}$).
Based on what you have written in the comments I interpret the question as which constraints are there on $A$ and $B$ such that there exists a $u(t) \in \cal{U}$ such that $x(t)$ can be driven to the origin for any possible $x_0\in\mathbb{R}^n$ in some finite amount of time.
It can be noted that bang-bang control is not directly relevant. Instead, null-controllability under input constraints is more suitable. Here null-controllability means that for an initial condition $x_0$ there exists some $T\in[0,\infty)$ such that there exists a $u(t) \in \cal{U}$ such that $x(T)=0$. And regarding bang-bang control, if $(1)$ can be driven to the origin using $u(t) \in \cal{U}$, then one of the possible inputs that does this can also be a bang-bang solution.
The short answer is that $(A,B)$ needs to be controllable and all the eigenvalues of $A$ are required to have a nonpositive real [1]. The full controllability is needed otherwise even without the constraint $u(t) \in \cal{U}$ it would not be possible to drive the state to the origin in some finite amount of time. There are no constraints on the multiplicity of the eigenvalues.
In order to see why multiplicity of the eigenvalues is not an issue I will consider only one real Jordan block with eigenvalues on the imaginary axis
$$ C = \begin{bmatrix} 0 & \omega \\ -\omega & 0 \end{bmatrix}, \quad A = \begin{bmatrix} C & I \\ & C & \ddots \\ & & \ddots & I \\ & & & C \end{bmatrix}, \quad B = \begin{bmatrix} 0 \\ \vdots \\ 0 \\ 1 \end{bmatrix}, \tag{2} $$
with $I$ the $2\times2$ identity matrix and $A$ having $m$ times $C$ along its diagonal (so $A\in\mathbb{R}^{2m\times2m}$). The solution for $x(t)$ using $(2)$ in $(1)$ can be expressed using the following convolution integral
$$ x(t) = e^{A\,t}x(0) + \int_0^t e^{A\,(t-\tau)} B\,u(\tau)\,d\tau, \tag{3} $$
where the matrix exponential of a Jordan block using the $A$ from $(2)$ can be shown to be
$$ e^{A\,t} = \begin{bmatrix} e^{C\,t} & t\,e^{C\,t} & \cdots & \frac{t^{m-1}}{(m-1)!}e^{C\,t} \\ & e^{C\,t} & \ddots & \vdots \\ & & \ddots & t\,e^{C\,t} \\ & & & e^{C\,t} \end{bmatrix}, \quad e^{C\,t} = \begin{bmatrix} \cos \omega\,t & \sin \omega\,t \\ -\sin \omega\,t & \cos \omega\,t \end{bmatrix}. \tag{4} $$
Even though $e^{C\,t}$ remains bounded, for $m>1$ some entries of $e^{A\,t}$ become unbounded due to the polynomial terms in $t$ (up to order $t^{m-1}$). In order to see that an unbounded $e^{A\,t}$ and thus unforced response $e^{A\,t}x(0)$ in not an issue for stabilizability of $x(t)$, while considering the input constraints $u(t) \in \cal{U}$, one can look at the second, convolution, term of $(3)$. Namely, in the case of $(2)$ if one chooses $u(t) = M\,\sin(\omega\,t+\phi)$, with $M$ chosen small enough such that $u(t) \in \cal{U}$, then the convolution term can also be obtained using an augmented autonomous state space model. This augmented model also uses $A$ from $(2)$ but has $m+1$ times $C$ along its diagonal with all initial condition equal to zero accept the bottom two entries, which represent $u(t)$. The resulting response al follows $(4)$, but since its size is larger it will have polynomials of one order higher. So, no matter how small $M$, eventually at large enough value for $t$ the response of the augmented model can be larger in magnitude than the unforced response. So eventually the reachable set from the convolution integral will grow faster in $t$ than the unforced response.
For example consider numerically solving the following optimisation problem obtained by first discretizing $(1)$ using $(2)$ with $\omega=1$, $k=3$, zero-order hold discretization and time step $\Delta t=0.1$, such that
$$ C = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}, \quad A = \begin{bmatrix} C & I & 0 \\ 0 & C & I \\ 0 & 0 & C \end{bmatrix}, \quad B = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}, \quad \begin{bmatrix} A_d & B_d \\ 0 & I \end{bmatrix} = e^{\begin{bmatrix} A & B \\ 0 & 0 \end{bmatrix}\Delta t}. $$
The optimisation problem is then defined as minimizing the following cost function
\begin{align} J =& \sum_{k=1}^{N} x_k^\top\,x_k, \\ \text{s.t.}\ & x_{k+1} = A_d\,x_k + B_d\,u_k, \\ & -0.3 \leq u_k \leq 0.3, \\ & x_0 = \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 \end{bmatrix}^\top. \end{align}
For $N=500$ the following numerical results can be obtained:
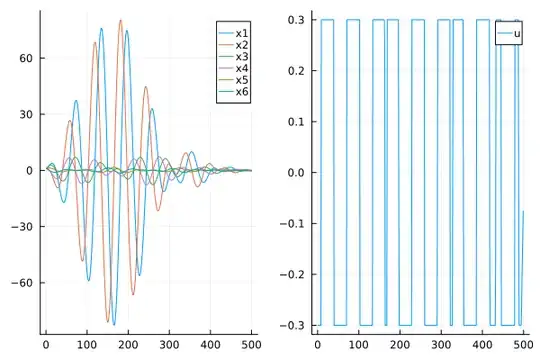
It can be noted that due to the oscillatory nature of this system, there is no upper bound on the number of switches between lower and upper bounds of the control input, when there is no bound on $\|x_0\|$.
[1]: Hu, T., Lin, Z., Hu, T., & Lin, Z. (2001). Null Controllability—Continuous-Time Systems. Control Systems with Actuator Saturation: Analysis and Design
- 12,770