Motion in a vertical circle (Mechanics / Physics) solution error?

Question

I wonder if someone would be kind enough to check a solution that I feel contains an error?

Question

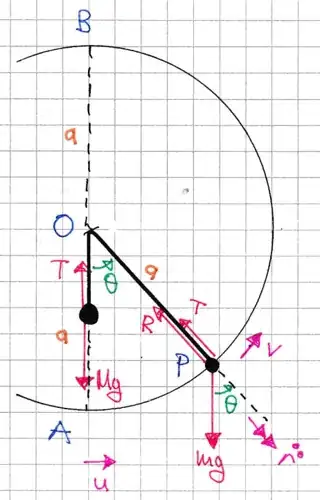
A small bead, of mass $m$, is threaded on a smooth circular wire, with centre $O$ and radius $a$, which is fixed in a vertical plane. You may further assume that the bead can freely access all parts of the vertically fixed wire.

A light inextensible string has one of its ends attached to the bead, passes through a smooth ring at $O$, and has its other end attached to a particle of mass $M$, which is hanging freely vertically below $O$.

The bead is projected from the lowest part of the wire with speed $u$ and makes complete revolutions passing through the highest part of the wire with speed $\sqrt{12ag}$.

Determine an expression for $u^2$, in terms of $a$ and $g$, and show that $11m \le M \le 17 m$.

(The question is number 7 on this paper: FM2)

Given solution

(For the full solution see FM2 Solutions) I write the main ideas here.

Let $\theta, v$ be defined in the diagram. Using conservation of energy, we have $v^2 = u^2 -2ag + 2ag\cos\theta$. Setting $v^2 = 12ag$ at $\theta = \pi$, we see that $u^2 = 16ag$. $\cdots (1)$.

We resolve forces radially. Let the positive direction be inwards. Let $T=Mg$ be the tension due to the string and $R$ the reaction force due to the hoop. Since the radial acceleration is $-v^2/a$ , we have $m(-v^2/a)=mg\cos\theta - Mg - R$ and thus using $(1)$, we have $R = 14mg + 3mg\cos\theta - Mg$. $\cdots (2)$

There exists some $\theta$ for which $R=0$, so $\cos\theta = (M-14m)/3m$ has a solution, so $11m\le M \le 17m$.

My problem

The bounds on $M$ is the part I have issue with.

Deriving up to $(2)$: $R=14mg+3mg \cos(\theta)- Mg$, is straightforward, but the subsequent analysis (specifically setting $R=0$) is the part of concern.

Given that the bead is fixed on the circular path and there is a tension towards the centre that will provide a component of the centripetal force, then the reaction force can be acting in either direction at any point.

At the top of the circle, as long as the net radial force is towards the centre, then the motion is possible, i.e. $R+Mg+mg=15mg + 3mg\times(-1)$ so we require $R+Mg+mg>12mg$, hence $R+Mg>11mg$.

Likewise at the lowest point we would have $R+Mg-mg=13mg+3mg\times 1$ ,so we require $R+Mg-mg>16mg$, hence $R+Mg>17mg$.

Given that $R$ can be acting either towards the centre or away from the centre, I cannot see the relevance of setting $R=0$.

Answer 1

I agree with your interpretation of the physics of the question. There is no reason to assume that there is ever an angle at which $R = 0$.

Since the velocity of the bead can be determined at every angle and the radial component of the bead's weight likewise can be determined at every angle, and since $T$ and $R$ are the only other forces on the bead, it is possible to determine the force $T + R - mg\cos\theta$ that is required to provide the necessary radial acceleration at every point along the bead's path.

If we assumed the bead had a coefficient of friction with the wire, the normal force $R$ between the wire and bead would be relevant to the tangential deceleration of the bead. But we seem to be assured that there is no friction.

There does not appear to be any other constraint on $R$ other than the formula $T + R - mg\cos\theta = mv^2/a.$ So we can set $T$ to any non-negative value we want (by choosing $M$; negative values are not possible) and then solve for $R.$

Perhaps there was originally meant to be an additional condition in the question that said the bead presses down on the wire (or the wire presses upward on the bead) at the top of the loop. Then it would be true that $R = 0$ at some point along the wire. But I don't see any such condition in the problem statement.

---

Here is a related problem where the idea that $R = 0$ is relevant:

A small bead, of mass $m$, is contained within a thin cylindrical drum with center $O$ and radius $a$, oriented so that the bead is constrained to a vertical plane. The bead may travel anywhere inside the drum.

A light inextensible string has one of its ends attached to the bead, passes through a smooth ring at $O$, and has its other end attached to a particle of mass $M$, which is hanging freely vertically below $O$.

The bead is projected from the lowest part of the drum with speed $4\sqrt{ag}$ in a direction tangent to the drum. Initially, the bead follows the curved surface of the drum, but before reaching the top of the drum the bead loses contact with the drum's curved surface.

Show that $11m \leq M \leq 17 m$.

Now $R = 0$ at the point where the bead loses contact with the curved surface. But in losing contact with the surface, the bead fails to reach the top of a circular path of radius $a,$ so we cannot say that its speed is $\sqrt{12ag}$ at the top of the loop.

I think that in writing this problem, someone either improperly combined some kind of problem like this with another problem or tried to turn such a problem into a two-parter by making the answer first compute the speed at the bottom, neglecting the fact that the modified problem no longer requires that $R = 0$ at any point.