1

Find analytically the two lines resulting from the intersection of the two cones sharing the same vertex.

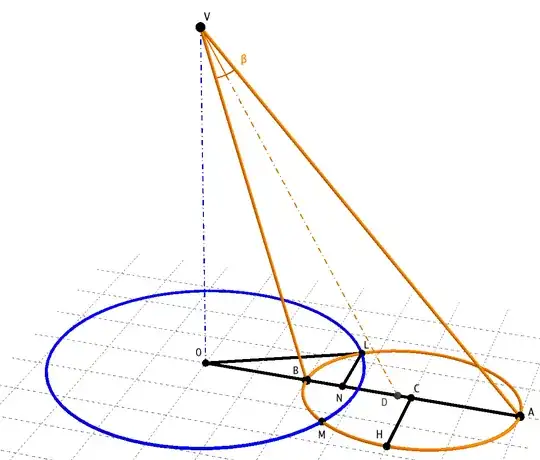
I am having trouble solving my problem. By developing a parametrization of the two cones and by looking for the equalities I fall on a trigonometric system without interest. Any idea ? enter image description here

Paprika7191
  • 2,741
CelmarCeaumar
  • 31
  • It seems that the two rays lie on the same plane - will a plane that intersects the two cones help? – Moti Apr 24 '23 at 18:14
  • Does this answer your question ? https://math.stackexchange.com/questions/4409846/equation-of-pair-of-lines-created-by-the-intersection-of-2-double-cones –  Apr 25 '23 at 06:10

1 Answers1

2

Consider the plane of the axes $VO$, $VD$ of the cones, and another plane perpendicular to $VO$ at $O$, intersecting the first cone on a circle of center $O$ (blue in figure below) and the second cone on an ellipse (orange).

Line $OD$ cuts the ellipse at the endpoints of major axis $AB$: knowing the apertures of the cones and the angle formed by their axes it is not difficult to find the positions of $A$, $B$ and of their midpoint $C$, which is the center of the ellipse.

The semi-major axis of the ellipse $a=AC=BC$ can then be computed, while the minor axis $b=CH$ is given by $$ b^2=VA\cdot VB\,\sin^2\beta, $$ where $\beta$ is the semi-aperture of the second cone (see here for a proof).

Let then $L$ and $M$ be the intersections of circle and ellipse, and $N$ their midpoint. If we set: $ON=x$, $LN=y$, $OC=d$, $OL=r$ we have: $$ y^2=r^2-x^2,\quad{(d-x)^2\over a^2}+{y^2\over b^2}=1. $$ Substituting $y^2$ from the first equation into the second one, we can find a quadratic equation for $x$ which can be solved.

enter image description here

Intelligenti pauca
  • 55,765