Mathematical Paradox: How Can The Center of a Shape Be Located OUTSIDE This Shape?

Question

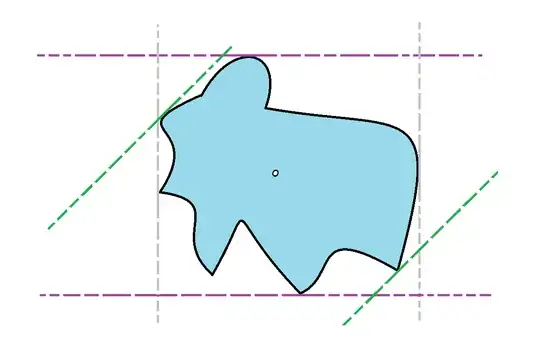
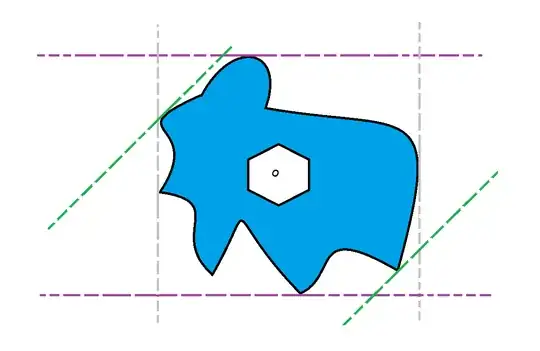
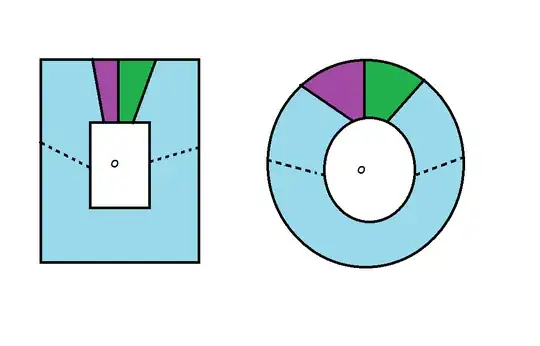
Recently I have been learning about Geospatial Analysis in which we are often interested in using computer software to analyze the mathematical properties and characteristics of polygons (e.g. calculating their centroids).

For example, using the R programming language, I downloaded a geospatial file of Canada that is broken up into different "polygons" - I then attempted to calculate the centroids of each of these polygons and visualize the results.

Here the Code :

    library(dplyr)
    library(sf)
    library(data.table)
    library(rvest)
    library(leaflet)
    library(ggplot2)
    library(urltools)
    library(leaflet.extras)
    library(stringr)
    library(magrittr)
# Download zip files
url_1 <- "https://www12.statcan.gc.ca/census-recensement/alternative_alternatif.cfm?l=eng&dispext=zip&teng=lada000b21a_e.zip&k=%20%20%20151162&loc=//www12.statcan.gc.ca/census-recensement/2021/geo/sip-pis/boundary-limites/files-fichiers/lada000b21a_e.zip"


download.file(url_1, destfile = "lada000b21a_e.zip")

# Extract zip files
unzip("lada000b21a_e.zip")

# Read shapefiles
ada <- st_read("lada000b21a_e.shp")

shapefile_1 = ada %>% st_transform(32617)
#sf_cent <- st_centroid(shapefile_1)

sf_cent <- st_point_on_surface(shapefile_1)

# Transform the centroids to the WGS84 CRS
sf_cent_geo <- st_transform(sf_cent, crs = 4326)


# Extract the longitude and latitude coordinates of the centroids
lon <- st_coordinates(sf_cent_geo)[,1]
lat <- st_coordinates(sf_cent_geo)[,2]

ADAUID <- sf_cent_geo$ADAUID
lon <- st_coordinates(sf_cent_geo)[,1]
lat <- st_coordinates(sf_cent_geo)[,2]

shapefile_1 = ada %>% st_transform(32617)
sf_cent <- st_centroid(ada)

ggplot() + 
    geom_sf(data = shapefile_1, fill = 'white') +
    geom_sf(data = sf_cent, color = 'red') 

The results look something like this:

As we can see, some of these polygons appear to have multiple centroids ("red points") - this means the centroids for some of these polygons are located outside of these polygons themselves!

Based on these two references here (https://en.wikipedia.org/wiki/Shoelace_formula, https://en.wikipedia.org/wiki/Centroid), the formula for calculating the centroid of a polygon can be written as such (based on the area of the polygon):

$$A = \frac{1}{2} | \sum_{i=1}^n (x_i y_{i+1} - x_{i+1} y_i) |$$

$$C_x = \frac{1}{6A} \sum_{i=0}^{n-1} ((x_i + x_{i+1}) (x_i y_{i+1} - x_{i+1} y_i))$$

$$C_y = \frac{1}{6A} \sum_{i=0}^{n-1} ((y_i + y_{i+1}) (x_i y_{i+1} - x_{i+1} y_i))$$

My Question: Is it possible to mathematically prove that sometimes $C_x$ and $C_y$ can be located outside the perimeter of the polygon that they belong to? Otherwise, how else is it possible that the centroid of a polygon can be located outside of the polygon itself?

Thanks!

Answer 1

I am going to answer the Question in the title & the last Sentences : "... Mathematically Prove that sometimes $C_x$ & $C_y$ can be located outside the Perimeter of the Polygon ..."

(1) In a way , It is not Possible for $C_x$ & $C_y$ to be outside the Zone (range) of "Perimeter of the Polygon" , these are always within that Zone. This might be the Core Point of Confusion.
I am using the word "Zone" to keep it Intuitive , there are technical ways to put it with Mathematical terminology later.

Consider this Blue Polygon (more generally : Shape/area/region) with Centeroid @ $O$ :

Then , $C_x$ , the x-Co-ordinate of $O$ , must be within the Gray lines.
More-over , $C_y$ , the y-Co-ordinate of $O$ , must be within the Purple lines.
In general , we can have Slanting Parallel lines (Eg the Green lines) touching the Polygon at the 2 Extremes , where we can say that $O$ & $C_x$ & $C_y$ must lie within those (Green) lines.
Thus , the Centeroid must lie within the "Zone".
Proving that is via Symmetry , Integration , linear Combinations , Etc.

(2) Must the Centeroid be a Part of the Polygon ? Not necessary ! It must be in the "Zone" but not necessarily within the Polygon !

Example 2.1:
Take the Earlier Image , Cut out a Part which has $O$ , then the Centeroid may move around a little , but it will be "outside" the area , though within the "Zone" !

Here , I have Cut out a Small Hexagonal area , hence $O$ will lie "outside" the Blue area , maybe moving around a little.

Example 2.2:
Consider Squares & Circles , where the Centeroid is at the Exact "Center".

We can cut out a smaller similar area at the Center , then the Centroid is outside , though still at the "Center". We can then cut out the Purple Part , which will make the top lighter , the bottom heavier , hence $C_y$ will move downward. It makes the left lighter, the right heavier , hence $C_x$ will move a little right.
We can then cut out the Green Part , which make the top lighter , hence $C_y$ moves downwards. It makes the left & right Equal weight , hence $C_x$ goes back.
With a large enough cut-out (Eg at the Dotted lines) , we can make the Centroid move downward back into the Blue area.

(3) Mathematically , we can state it like this :
In all these Cases , $O$ can not occur outside the "Zone" :
$x_{min} \le C_x \le x_{max}$
$y_{max} \ge C_y \ge y_{min}$
In other words , we take the whole Polygon / area / region & take the minimum values & maximum values of $x$ & $y$ , then we know where the Centeroid must occur. The Exact values can be computed using various formulas.
Without knowing the Exact Polygon , we might make quick inaccurate approximations like $C_x = [ x_{min} + x_{max} ] / 2$ & $C_y = [ y_{max} + y_{min} ] / 2$ , though that is very rarely the Case.