A light is at the top of a pole $50$ft high. A ball is dropped from the same height from a point $30$ft away from the light. How fast is the shadow of the ball moving along the ground $1\over 2$ seconds later? (Assume the ball falls a distance $s = 16t^2$ft in $t$ seconds.)
The way I attempted at this is as so:
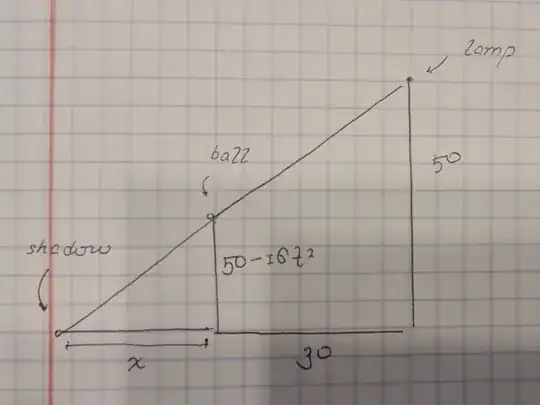
The geometrical picture we are looking at is of two heights ($= 50$ft) $30$ft horizontally away from each other. One of the heights decreases towards the horizontal at a rate $-16t^2$. As this height decreases, connect the tips of both heights with a line and produce this line till it hits the horizontal. Call the length between the point at which the line hit the horizontal and the foot of the decreasing height $x$. Then the tip of this length is the shadow of the ball, and it is required to find the rate at which this length decreases. The image below should provide a visual aid:
Call the balls height from the horizontal $y$ (this is $50 - 16t^2$ on the picture), then by what is given, ${dy\over dt}=-32t$ (since $y = 16t^2$)
An obvious relation between the variables and the constants is of the proportionality between the sides of the triangles.
${x\over y} = {x + 30 \over 50}$
Solving for $x$, $x = {30y \over 50 - y}$
Implicitly differentiating, $x^\prime = 30y(50 - y)^{-2}y^\prime + (50 - y)^{-1}30y^\prime$
Substituting for $y^\prime = -32$, we get $x^\prime = -1500$.
Is this result correct? I must ask for I do not consider myself yet experienced, hence I have to get constant affirmation from those more professional. Thank you in advance.
\overis a tricky macro, as you discovered. I prefer\frac, for example,\frac{x}{y}. Also, whatever you were using for the negative sign, just use an ordinary old ASCII hyphen instead; it will typeset much better. – David K Apr 17 '23 at 16:13