0

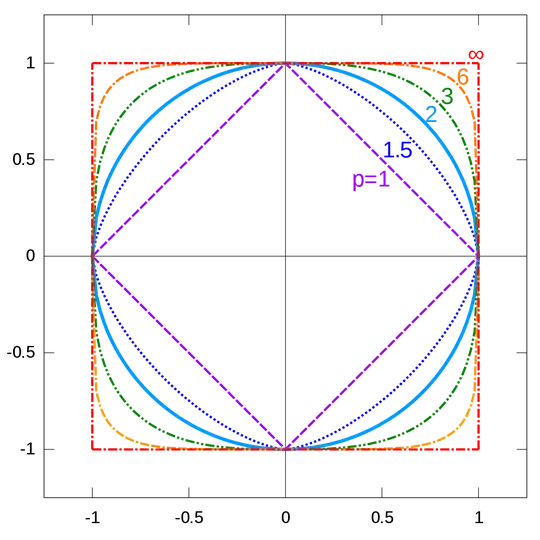
Consider the below figure drawing some examples of unit balls for various $L_p$ metrics.

For $p=1$ and $p=\infty$ we get squares (hyperoctahedra and hypercubes in higher dimensions, respectively), and when $p=2$ we get a circle (spheres in higher dimensions).

For intermediary values of $p$, how would one describe what shape these balls are?

Would they be considered ellipses?

enter image description here

R. H. Vellstra
  • 3,263
  • 2
    Popular term: superellipse ($d=2$) and superellipsoid ($d > 2$). https://en.wikipedia.org/wiki/Superellipse . Also "Lamé curve" ($d=2$). – GEdgar Apr 15 '23 at 01:25
  • Ah, thank you @GEdgar - this is exactly what I was looking for and opens the door to learn more about these kinds of shapes. – R. H. Vellstra Apr 15 '23 at 01:28
  • That article says the case $d=2, p=4$ is called a "squircle". But I must admit I have not heard this term elsewhere. – GEdgar Apr 15 '23 at 01:32
  • I noticed that. Apparently squircles generalize to spherical cubes, or "hypersphubes" (at least according to someone!). https://en.wikipedia.org/wiki/Squircle#p-norm_notation – R. H. Vellstra Apr 15 '23 at 01:34
  • You might be interested in this post. – Ng Chung Tak Apr 15 '23 at 06:23

0 Answers0