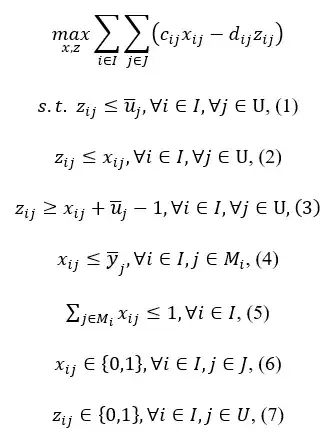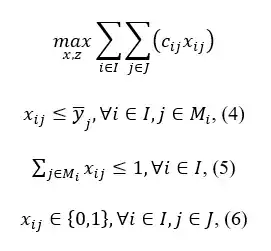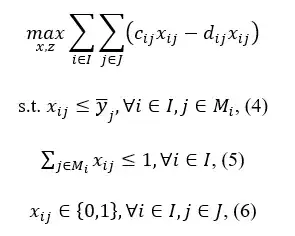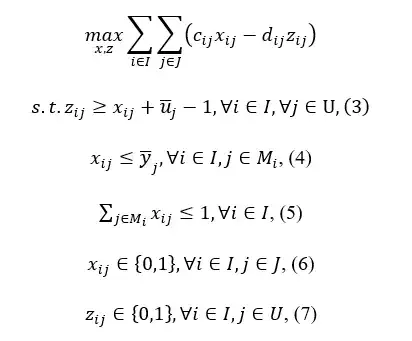0

For the following problem, can we say that its linear relaxation is equivalent to the binary problem?

Problem 1 ($y_j$ and $u_j$ are $0-1$ parameters.):

enter image description here

Given that $u_j=0$ the problem becomes (as $z_{ij}$ becomes zero): Problem (2)

enter image description here

Given that $u_j=1$ the problem becomes (as $z_{ij}$ becomes equal to $x_{ij}$ because of constraints 2 and 3): Problem (3)

enter image description here

Can we say that the linear relaxation of the main problem (Problem 1) is equivalent to itself? (Is the integrality gap 0?).

P.S. I will write the questions in the screenshots when I have more time.

Edit: Problem 4

$1 \geq c_{ij} \geq d_{ij} \geq 0$

enter image description here

Since the Problem 1 is maximization type and $d_{ij} \geq 0$ we can further remove constraints (1) and (2) and obtain Problem 4. I think the same rules should apply to it and we should be able to safely use its dual in Benders (as dual subproblem) and it should give the exact same answer. However, according to my computations, it is not the case. It kind of feels strange. It is probably related to the cuts added to the master problem, but could not be exactly sure. Do you see any reason why this could happen, do you have any explanations?

madetolast
  • 123

1 Answers1

1

Yes, for fixed $\bar{u}$ and $\bar{y}$, the problem decomposes into a separate problem for each $i$. Each such problem can be solved by inspection, and the optimal objective value is attained by integer $x$.

RobPratt
  • 50,938
  • So, it would be safe to take the dual of problem 1 to use as dual subproblem in Benders. Am I correct? – madetolast Apr 12 '23 at 04:59
  • 1
    Yes, that is correct. – RobPratt Apr 12 '23 at 05:15
  • Relaxing the problem 1 and using its dual as the dual subproblem in Benders gives correct results. However, I added one more question (Problem 4) to the main post which seems a little counter-intuitive. If you could take a look I would be very glad. @RobPratt – madetolast Apr 12 '23 at 19:35
  • 1
    Yes, if $d$ is nonnegative, Problems 1 and 4 should yield the same optimal objective values. As a check, you might try solving them both directly, without Benders. – RobPratt Apr 12 '23 at 21:59
  • Yes, they give the same objective values for the primal problems. However, when I use them as dual subproblems of Benders, Problem 4 leads to inaccurate results. I think it could be related the cuts added to the master problem, but I could not be sure. – madetolast Apr 12 '23 at 22:31
  • 1
    Because $x=z=0$ is always feasible, you need only Benders optimality cuts (and not Benders feasibility cuts). I recommend rewriting your problem in standard form with $\le$ constraints, all $x$ and $z$ variables on the LHS, and all constants (including fixed variables) on the RHS. – RobPratt Apr 12 '23 at 23:30
  • You are correct, I was mistaken. I have one more question, do you think that it is never possible $x_{ij}$ to take fractional values, even if multiple $x_{ij}$s have the same objective coefficients? Would it always have to be integer? If it could be fractional, would it be ok to use its dualized subproblem in Benders? @RobPratt – madetolast Apr 15 '23 at 21:48
  • 1
    If your solver doesn’t return a basic solution, you can get fractional values, but there will always exist an integer optimal solution, and you can still use the dualized subproblem anyway. – RobPratt Apr 15 '23 at 21:55
  • About using the dualized subproblem, wouldn't the optimality cuts be affected if the $x_{ij}$ values are fractional rather than integers? Wouldn't it affect the solution? If not, how can I prove that? – madetolast Apr 15 '23 at 22:33
  • 1
    Benders cuts generated from fractional master solutions are still valid. You can use any relaxation for the master problem. One type of relaxation omits constraints, and another type relaxes integrality. You can do both at the same time. – RobPratt Apr 15 '23 at 23:55
  • I see, but Problem 4 is not the master problem, it is the subproblem. Master problem is a decision problem to obtain $u_j$ and $y_j$. – madetolast Apr 16 '23 at 06:48
  • 1
    Yes, sorry for the confusion. From the subproblem, you just need the dual variables, which you can access as a byproduct of solving the primal form of the subproblem as LP or directly by solving the dual form of the subproblem LP. – RobPratt Apr 17 '23 at 17:57
  • I see, so you mean it would not create a problem if we take the dual variables ensuring that the primal subproblem has integral $x_{ij}$ values, am I correct? After solving the primal subproblem and ensuring all $x_{ij}$ are integral, I think I can do that by complementary slackness theorem. Do you know if there is a way we can do it while solving the dualized subproblem? – madetolast Apr 18 '23 at 18:34