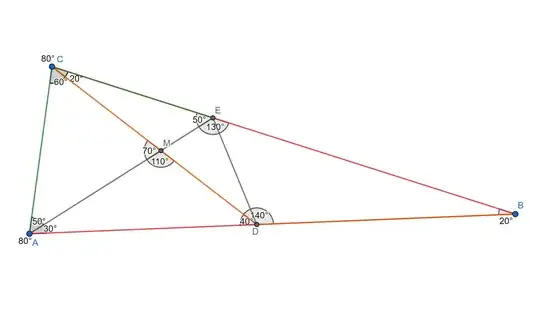
While I was going through some problems of the maths olympiad, I came across a problem where concrete angles of a specific triangle were given, which was not typical for a maths olympiad question. Yet I did not manage to solve this problem. It goes as follows:
In an isosceles triangle $\triangle ABC$ with base $\overline{AC}$, the angle $\angle CBA$ is $20°$. $D$ is a point on $\overline{AB}$ so $\angle ACD$ is $60°$ and $E$ is a point on $\overline{BC}$ so $\angle EAC$ is $50°$. What is the size of $\angle EDC$?
This is about how far you can get by using basic theorems to solve for angles:
But I couldn't do much other than notice that $\triangle ACE$ and $\triangle CDB$ are isosceles triangles. My instinct says that the solution might involve cyclic quadrilaterals and the intercept theorem, the triangles $\triangle AEB$ and $\triangle CED$ look like they're similar, but I'm unable to prove that they are.
Thanks!