Direct proof for the chi-square value being chi-square distributed with one degree of freedom for a 2x2 contingency table

Question

for a 2x2 contingency table, we have for the observed and expected frequencies the following:

We require e.g. that 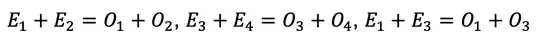which are that the row and column sums have to match between observed and expected frequencies where for the expected frequencies are calculated as e.g. here https://en.wikipedia.org/wiki/Pearson%27s_chi-squared_test#Testing_for_statistical_independence. With the three equations, we can calculate the forth one. Further more, with these three equations, we can transform the chi-square sum as follows 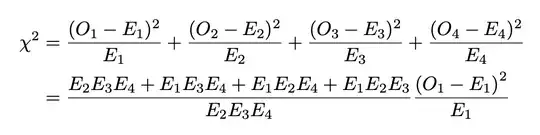by making a common denominator and using the identities for differences between the observed and expected frequencies from the requirement. The term 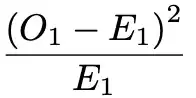is clearly chi-square distributed with one degree of freedom by definition. However, what is the argument why the factor in front of it 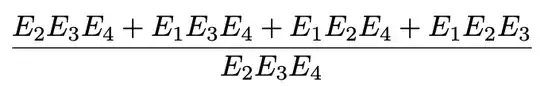does not change the distribution for the total equation?

Is there a change to see that it converges against 1 at least for large expected frequencies or is there a more abstract argument why in spite of that (scaling) factor the second equation in the chi-square calculation is still chi-square distributed with one degree of freedom?

I find only very abstract proofs of the degrees of freedom for a test of independence with a chi-square test in textbooks. So I thought a direct calculation might help to understand this issue of degrees of freedom better. However, I cannot make the last conclusion in this example. So I am very happy for your help.

Thank you

Tim

Answer 1

Let us begin with the definitions:

$$ E_{1}:=(O_{1}+O_{3})\frac{O_{1}+O_{2}}{N},\ E_{2}:=(O_{2}+O_{4})\frac{O_{1}+O_{2}}{N},\ E_{3}:=(O_{1}+O_{3})\frac{O_{3}+O_{4}}{N},\ E_{4}:=(O_{2}+O_{4})\frac{O_{3}+O_{4}}{N} $$

With the requirement

$$ O_{1}+O_{2}+O_{3}+O_{4}=N $$

we can conclude:

$$ E_{1}+E_{2}=O_{1}+O_{2},\ E_{3}+E_{4}=O_{3}+O_{4},\ E_{1}+E_{3}=O_{1}+O_{3},\ E_{2}+E_{4}=O_{2}+O_{4} $$

From this, it follows:

$$ E_{2}-O_{2}=O_{1}-E_{1},\ E_{3}-O_{3}=O_{1}-E_{1},\ E_{4}-O_{4}=O_{2}-E_{2}=E_{1}-O_{1} $$

with which we can calculate:

$$ \begin{split}\chi^{2} & =\sum_{i=1}^{4}\frac{(O_{i}-E_{i})^{2}}{E_{i}}\\ & =\frac{(O_{1}-E_{1})^{2}}{E_{1}}+\frac{(O_{1}-E_{1})^{2}}{E_{2}}+\frac{(O_{1}-E_{1})^{2}}{E_{3}}+\frac{(O_{1}-E_{1})^{2}}{E_{4}}\\ & =\left(1+\frac{E_{1}}{E_{2}}+\frac{E_{1}}{E_{3}}+\frac{E_{1}}{E_{4}}\right)\frac{(O_{1}-E_{1})^{2}}{E_{1}}\\ & =\left(\frac{E_{2}E_{3}E_{4}+E_{1}E_{3}E_{4}+E_{1}E_{2}E_{4}+E_{1}E_{2}E_{3}}{E_{2}E_{3}E_{4}}\right)\frac{(O_{1}-E_{1})^{2}}{E_{1}} \end{split} $$

Let us assume that the $E_i, i\in{1,2,3,4}$ are large enough such that $\frac{(O_{i}-E_{i})^{2}}{E_{i}},i\in\left\{ 1,2,3,4\right\}$ are normally distributed. Is there a way to see or to rewrite some of the equation such that we see that the right hand side is chi-square distributed with one degree of freedom? If yes, we could generalize this calculation to a direct proof of the degrees of freedom for the chi-square test of independence.

Answer 2

Simply put, the values $E_i$ for $i \in \{1, 2, 3, 4\}$ are not random variables. Only the observed quantities $O_i$ are random variables. The $E_i$ relate to what we expect the frequency counts to be for a given sample size $n$. For an experiment with a predetermined number of observations, they will not change from experiment to experiment, whereas the $O_i$, the observed cell frequencies, may change due to the randomness inherent in the sampling process.

Consequently, the distributional properties of the statistic $\chi^2$ do not depend on any constant factors with respect to the $O_i$.

Answer 3

(It's not clear how to obtain the equation you quoted involving denominator $E_2E_3E_4$; is there a source for this result?)

In a $2\times 2$ contingency table the test statistic $\sum_{i=1}^4\frac{(O_i-E_i)^2}{E_i}$ has approximately a chi-square distribution with one degree of freedom. Here is a derivation, using slightly different notation. The derivation is all algebra.

Suppose you have split a population of $N$ individuals into two groups, and counted the number of "positives" vs "negatives" among the two groups, obtaining a $2\times 2$ contingency table: $$ \begin{array}{|c|c|c|c|} \hline &\text{Group 1}&\text{Group 2}\\ \hline \text{Positive}&a & b\\ \text{Negative}&c & d\\ \hline &n_1:=a+c&n_2:=b+d&N:=n_1+n_2\\ \hline \end{array} $$ Start with the identity $$\sum_{i=1}^4\frac{(O_i-E_i)^2}{E_i}=\frac{N(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}. $$ Now let $p_1:=\frac a{n_1}$ be the observed proportion of positives in group 1, and let $p_2:=\frac b{n_2}$ be the observed proportion of positives in group 2, and define $q_1$ and $q_2$ similarly to be the observed proportions of negatives. We can express the cell counts in terms of these new variables: $$ \begin{array}{|c|c|c|c|} \hline &\text{Group 1}&\text{Group 2}\\ \hline \text{Positive}&a=n_1p_1 & b=n_2p_2\\ \text{Negative}&c=n_1q_1 & d=n_2q_2\\ \hline &n_1&n_2&N\\ \hline \end{array} $$ Substitute these values into the identity and simplify: $$ \begin{aligned} \sum_{i=1}^4\frac{(O_i-E_i)^2}{E_i}&=\frac{N(n_1p_1n_2q_2-n_2p_2n_1q_1)^2}{(n_1p_1+n_2p_2)(n_1q_1+n_2q_2)(n_1)(n_2)}\\ &=\frac{Nn_1n_2(p_1 q_2-p_2q_1)^2}{(n_1p_1+n_2p_2)(n_1+n_2-(n_1p_1+n_2p_2))} \end{aligned} $$ Writing $N=n_1+n_2$, and noting that that $p_1q_2-p_2q_1=p_1(1-p_2)-p_2(1-p_1)=p_1-p_2$, and defining $p:=(n_1p_1+n_2p_2)/(n_1+n_2)$ (the pooled estimate of the proportion of positives), this equals $$\frac{(n_1+n_2)n_1n_2(p_1-p_2)^2}{(n_1+n_2)p(n_1+n_2)(1-p)}=\left(\frac{p_1-p_2}{\sqrt{p(1-p)\left(\frac1{n_1}+\frac1{n_2}\right)}}\right)^2 $$ which is the square of the $z$ test statistic for comparing two proportions. The $z$ test statistic has approximately standard normal distribution, hence its square has approximately chi-square distribution with one degree of freedom. (By definition, $\chi^2$ is the distribution of the square of a standard normal variable.)

---

Added: In what sense is the $z$ distribution approximately standard normal? The $z$ statistic converges in distribution to $N(0,1)$ as $n_1$ and $n_2$ tend to infinity -- under the null hypothesis that the population frequencies are equal for group 1 and group 2. This fact follows from the Central Limit Theorem and Slutsky's theorem. The argument is similar to that for the single-sample test of proportions. Note that the $p_1$ and $p_2$ named above are the sample proportions, i.e., observed from the data; they are not the population proportions.