Consider the following function $$ f(x,n)=\frac1x\sum_{k=0}^n\frac{e^{-k^2x}-e^{-(k+1)^2x}}{2k+1} $$ For small $x$, is there a way of approximating $f(x,n)$ by something like an inverse power law on $x$, depending on $n$. I am looking for something in the form $f(x,n)\simeq \alpha(n) x^{\beta(n)}$. If not, is there any function that approximates $f$, simplifying the expression on the RHS?
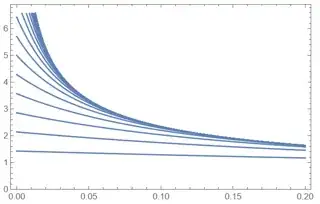
Note: For multiple various of $n$, for example, here are the plots of the family of functions defined by $f(x,n)$
Also, the limit $n\to\infty$ was studied for a similar function here ($xf(x,n)$).
My attempt: We can rewrite the summand as $$ \frac{e^{-k^2x}(1-e^{-(2k+1)x})}{2k+1} $$ Now, we can use the Taylor expansion of the exponential function $e^x \approx 1 + x$ for small $x$. We then get $$ 1-e^{-(2k+1)x}\approx (2k+1)x. $$ Thus, for small $x$, the summand becomes $$ \frac{e^{-k^2x}(2k+1)x}{2k+1}\approx e^{-k^2x}x $$ Using this approximation, we can rewrite the original function as $$ f(x,n)\approx \frac1x \sum_{k=0}^n e^{-k^2x}x=\sum_{k=0}^n e^{-k^2x} $$ This expression is simpler than the original one, although it's not in the form of an inverse power law. Any ideas on how to work it further?