Find the shortest distance between the circle $x^2+y^2-24x+128=0$ and the curve given by the locus of P.

Question

Four normals are drawn to the rectangular hyperbola $xy=c^2$ from a point $P(h,k)$. Find the shortest distance between the circle $x^2+y^2-24x+128=0$ and the curve given by the locus of P.

My Attempt:

Let a point on the hyperbola be $(ct,\frac ct)$

Equation of normal at this point is $xt^3-ty-ct^4+c=0$

It passes through $(h,k)$, so,

$ht^3-tk-ct^4+c=0$

This is biquadratic in $t$. Four roots will be the feet of normals from P.

Also, the circle and hyperbola cut each other in four points. Mean of those points is same as the mid point of the line joining the centres of circle and hyperbola.

Also, the required shortest distance will lie along the normal of circle and the curve given by locus of P.

Normal of circle passes through centre of circle.

Edit:

Locus of P is a straight line?

$$xt^3-yt-ct^4+c=0$$

Finding its distance from the centre of circle i.e. $(12,0)$

$$|\frac{12t^3-ct^4+c}{\sqrt{t^6+t^2}}|$$

We need to minimize it w.r.t $c$?

Taking the positive sign of the mod, I am differentiating the above expression w.r.t $c$, thus,

$$\frac{-t^4+1}{\sqrt{t^6+t^2}}=0$$

So, $t=1$

Putting that in the distance, I get $\frac{12}{\sqrt2}=6\sqrt2$

Subtracting radius of the circle from it, I get

$$6\sqrt2-4=2\sqrt2(3-\sqrt2)$$

But the answer given is $4(\sqrt5-1)$

Edit $2$:

Locus of P won't be a straight line. As we need the locus of that point of intersection for which four normals exist. In any case, locus should be free of parameters.

So, for $f(t)= ct^4-ht^3+kt-c$ to have four roots, $f'(t)$ should have three roots (along with other conditions).

$f'(t)= 4ct^3-3ht^2+k$

For $f'(t)$ to have three roots, $f''(t)$ should have two roots (along with other conditions)

$f''(t)=12ct^2-6ht$

$f''(t)=0$ at $t=0, \frac{h}{2c}$

For $f'(t)$ to have three roots, $f'(0)f'(\frac{h}{2c})\lt0$

So, $k(k-\frac{h^3}{4c^2})\lt0$

Don't know what to do with it.

Answer 1

Hint: The discriminant is $c(-4x^3y^3+27x^4c^2-6x^2y^2c^2+27y^4c^2-192xyc^4+256c^6)=0.$

Answer 2

The equation of the circle can be written as $(x-12)^2+y^2=4^2$, so its center is $(12,0)$.

As you wrote, the required shortest distance will lie along the normal of circle and the curve given by locus of $P$.

So, let $Q(12+4\cos\theta,4\sin\theta)$ be a point on the circle.

Also, let $R(12+p\cos\theta,p\sin\theta)$ be a point on the curve given by the locus of $P$.

As you wrote, we have $$ct^4-ht^3+kt-c=0\tag1$$ We also have $$h=12+p\cos\theta\qquad\text{and}\qquad k=p\sin\theta\tag2$$

As a result, our problem is reduced to finding the minimum value of $QR=|p-4|$ under the condition that $(p,\theta)$ is such that $$ct^4+(-12-p\cos\theta)t^3+(p\sin\theta)t-c=0\tag3$$ has four distinct real roots $t$.

So, according to wikipedia, our problem is reduced to finding the minimum value of $|p-4|$ under the condition that

$$\begin{cases}-256c^{6}+192c^{4}(12+p\cos\theta)p\sin\theta-27c^{2}p^4\sin^4\theta \\\quad +6c^2(12+p\cos\theta)^2 p^2\sin^2\theta-27(12+p\cos\theta)^4c^{2} \\\quad +4(12+p\cos\theta)^3p^3\sin^3\theta\gt 0 \\\\p\cos\theta\not=-12 \\\\64c^4-16(12+p\cos\theta)c^2p\sin\theta+3(12+p\cos\theta)^4\gt 0\end{cases}$$

---

Example : Taking $p=4$ and $\theta=\frac{\pi}{2}$, we get $$0\lt c\lt 2\sqrt{3 (1 - 2^{4/3} + 2^{2/3})}\approx 0.900393$$

So, one can at least say that for $0\lt c\lt 2\sqrt{3 (1 - 2^{4/3} + 2^{2/3})}\approx 0.900393$ and $(h,k)=(12,4)$ which is on the circle, there are four normals, and the shortest distance is $0$.

---

the answer given is $4(\sqrt5-1)$

From what I've got, I don't think that the answer is $4(\sqrt5-1)\approx 4.944272$.

---

Added :

Can we make use of the following link? As I am trying to avoid the discriminant method because that's not in the syllabus. Where would the four normals be?

• The OP of the question says "I managed to prove that if $y>0$, then this quartic has 4 distinct real roots if $y<-\frac{1}{4c^2}x^3$ ".
  However, this is not true. For $(c,h,k)=(2,12+20\cos\frac{8\pi}{9},20\sin\frac{8\pi}{9})$ which satisfies both $k>0$ and $k<-\frac{1}{4c^2}h^3$, the equation has only two real roots. (see here)

• The OP says "I have attached a computer generated diagram for the case when $c=2$ at the bottom of this post".
  However, the diagram is not correct. As pointed out in a comment there, taking the point $(−2,0)$ in the blue area, the equation has only two real roots. (see here)

Also, I think that none of the answers there shows a necessary and sufficient condition.

Therefore, I don't think that we can make use of the link.

You are saying "I am trying to avoid the discriminant method". Fine, but then, I think that you cannot get a necessary and sufficient condition. We may be able to get a necessary (not sufficient) condition without using the discriminant, but if you want to get a necessary and sufficient condition (which is needed to solve your question), I think that you cannot avoid the discriminant method.

You might want to consider the following point :
You wrote "the statement is complete" and "the answer given is $4(\sqrt5-1)$". I would say that at least one of the two comments is incorrect (or textbook typo?) since for $c=\frac 12$ and $(h,k)=(12,4)$ which is on the circle, there are four normals, and the shortest distance is $0$.

---

In the following, let us consider the case $c=2$.

For $c=2$, writing $p=y$ and $\theta=x$, we want to find the minimum value of $|y-4|$ under the condition that $$\begin{cases}-16384+3072(12+y\cos x)y\sin x-108y^4\sin^4x \\\quad +24(12+y\cos x)^2 y^2\sin^2x-108(12+y\cos x)^4 \\\quad +4(12+y\cos x)^3y^3\sin^3x\gt 0 \\\\y\cos x\not=-12 \\\\1024-64(12+y\cos x)y\sin x+3(12+y\cos x)^4\gt 0\end{cases}$$

WolframAlpha gives

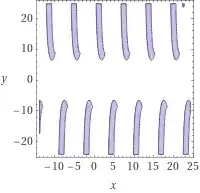
• If $y=6.5$, there is no such $x$.

• If $y=6.525$, then is no such $x$.

• If $y=6.55$, $x=\frac{17}{30}\pi$ satisfies the condition.

These should imply that there is $6.525\lt y_0\leqslant 6.55$ such that the minimum value of $|y-4|$ is $y_0-4$.