Proof of Riemann's theorem of Rudin how to show that $\alpha$ and $\beta$ are the $\lim \sup$ and $\lim \inf$ - need help to end my proof

Question

Here is the text of Rudin, Principles of Mathematical Analysis, chapter $3$, theorem $3.54$:

Let $\sum a_n$ be a conditionally convergent series. Suppose : $$ -\infty \leq \alpha\leq \beta \leq +\infty$$ Then there exist a rearrangement $\sum a'_n$ with partial sums $\{s'_n\}$ such that

$$ \lim\limits_{n\to\infty} \inf s'_n=\alpha \quad \quad \lim\limits_{n\to\infty}\sup s'_n=\beta$$ Let $$p_n = \frac{|a_n| + a_n}{2}, \ q_n = \frac{|a_n| - a_n}{2} \ (n = 1, 2, 3, \ldots). $$ Then $p_n - q_n = a_n$, $p_n + q_n = |a_n|$, $p_n \geq 0$, $q_n \geq 0$. The series $\sum p_n$, $\sum q_n$ must both diverge.

For if both were convergent, then $$\sum \left( p_n + q_n \right) = \sum |a_n|$$ would converge, contrary to hypothesis. Since $$ \sum_{n=1}^N a_n = \sum_{n=1}^N \left( p_n - q_n \right) = \sum_{n=1}^N p_n - \sum_{n=1}^N q_n,$$ divergence of $\sum p_n$ and convergence of $\sum q_n$ (or vice versa) implies divergence of $\sum a_n$, again contrary to hypothesis.

Now let $P_1, P_2, P_3, \ldots$ denote the non-negative terms of $\sum a_n$, in the order in which they occur, and let $Q_1, Q_2, Q_3, \ldots$ be the absolute values of the negative terms of $\sum a_n$, also in their original order.

The series $\sum P_n$, $\sum Q_n$ differ from $\sum p_n$, $\sum q_n$ only by zero terms, and are therefore divergent.

We shall construct sequences $\{m_n \}$, $\{k_n\}$, such that the series $$ P_1 + \cdots + P_{m_1} - Q_1 - \cdots - Q_{k_1} + P_{m_1 + 1} + \cdots + P_{m_2} - Q_{k_1 + 1} - \cdots - Q_{k_2} + \cdots \tag{25}, $$ which clearly is a rearrangement of $\sum a_n$, satisfies (24).

Choose real-valued sequences $\{ \alpha_n \}$, $\{ \beta_n \}$ such that $\alpha_n \rightarrow \alpha$, $\beta_n \rightarrow \beta$, $\alpha_n < \beta_n$, $\beta_1 > 0$.

Let $m_1$, $k_1$ be the smallest integers such that $$P_1 + \cdots + P_{m_1} > \beta_1,$$ $$P_1 + \cdots + P_{m_1} - Q_1 - \cdots - Q_{k_1} < \alpha_1;$$ let $m_2$, $k_2$ be the smallest integers such that $$P_1 + \cdots + P_{m_1} - Q_1 - \cdots - Q_{k_1} + P_{m_1 + 1} + \cdots + P_{m_2} > \beta_2,$$ $$P_1 + \cdots + P_{m_1} - Q_1 - \cdots - Q_{k_1} + P_{m_1 + 1} + \cdots + P_{m_2} - Q_{k_1 + 1} - \cdots - Q_{k_2} < \alpha_2;$$ and continue in this way. This is possible since $\sum P_n$, $\sum Q_n$ diverge.

If $x_n$, $y_n$ denote the partial sums of (25) whose last terms are $P_{m_n}$, $-Q_{k_n}$, then $$ | x_n - \beta_n | \leq P_{m_n}, \ \ \ |y_n - \alpha_n | \leq Q_{k_n}. $$ Since $P_n \rightarrow 0$, $Q_n \rightarrow 0$ as $n \rightarrow \infty$, we see that $x_n \rightarrow \beta$, $y_n \rightarrow \alpha$.

Finally, it is clear that no number less than $\alpha$ or greater than $\beta$ can be a subsequential limit of the partial sums of (25).

I have tried to prove the last two lines of the theorem (from "Finally, it is clear" until the end) but I could use some help in order to formalize the end of my proof.

Proof (inspired from this answer):

Since the series $s_n$ converges $a_n\to 0$, thus $\forall \epsilon >0$ there is an $N$ such that for all $n\geq N$, $$|a_n|<\epsilon$$

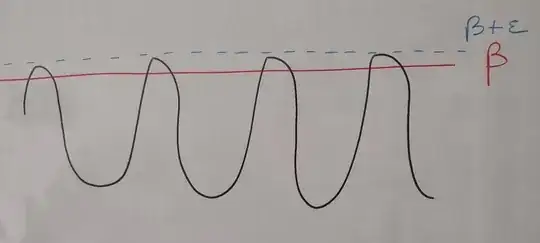
Now, consider the quantity $s_n' - \beta $. (We will only treat the case of $\beta$ and show that $s_n' \leq \beta $ for every $n$ superior to a certain $N$)

• If $\alpha = \beta$ we have $\lim \sup s_n' = \lim \inf s_n'$ hence, the limit of $s_n '$ is unique (and we don't need to prove that no number less than α or greater than β can be a subsequential limit of the partial sums).
• If $\alpha \neq \beta $, $s_n'$ "oscillates" between $\alpha$ and $\beta$ and its curve is made of peaks (that I drew in the figures below).

$s_n'$ can either coincide with a peak (in which case, there exists $m\in \mathbb N$ such that $s_n' = x_m$) or either not.

• If there exists $m$ such that $s_n' = x_m$ then there exists $N\in \mathbb N$ such as $$s_n'-\beta = s_n' - \beta _n + \beta _n -\beta < P_{m_n} + \frac{\epsilon}{2} < \frac{\epsilon}{2} + \frac{\epsilon}{2} < \epsilon $$ for every $n\geq N$

• If $s_n'$ is not a peak, then $s_n' - \beta = s_n ' - x_n + x_n - \beta$. This boils down to the previous case, as long as we can prove $s_n' - x_n \leq 0$. This where I could use some help to formalize things.

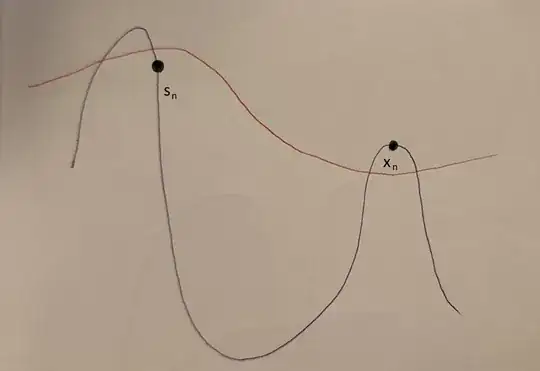$s_n$ is not inferior than $x_n$. Drawing of $s_n$ oscillating in blue and $\beta _n$ in red" />

As this picture shows, $s_n'$ is not necessarily inferior than $x_n$. Because $s_n'$ can be besides the summit of the previous peak. Previous peak, that is bigger than the peak of $x_n$.

However, at infinity it seems that $s_n' - x_n \leq 0$. For the good reason that all the peaks have about equal heights and that $s_n'$ can't find itself in the same configuration as in the previous picture.

Question:

Is there a way to be more precise, and show analytically (not with a graph) that $s_n' - x_n \leq 0$ for every $n \geq N$ ($N\in \mathbb N$) ?

Answer 1

I call this problem the creative accountant's dream problem.

Given an infinite collection of daily paper losses and paper profits, both of which add up to infinite losses and profits, the accountant is tasked with recording these values in an order so that the sequence of net proceeds converges to any pre-assigned final target value. (Math can either make you very wealthy or put you in jail).

I suggest drawing a diagram to organize your thoughts. Sort the positive terms in non-increasing order as $a_1 \geq a_2 \geq a_3\ldots$ and likewise for the negative terms $\{-b_k\}$, sort their magnitudes as $b_1\geq b_2, \ldots$. Then construct the sequence of partial sums $A_k =\sum_1^k a_j$ and likewise $B_k$. If both partial sum sequences converge, the series is absolutely convergent. If exactly one converges, then the other diverges, and their sum diverges.

So focus on the case where both sequences diverge. Plot these partial sums on two orthogonal axes. The gridlines on this diagram intersect in ordered pairs of "lattice points" that travel to infinity. The rectangles on this grid have their two dimensions decreasing as we travel rightward and/or upward. The goal is to show that we can obtain any preassigned limit value $L =\lim _{k\to \infty} A_{m_k} - B_{n_{k}}$ using some subsequence of lattice points. Here $(m_k, n_k)$ label the lattice points.

Draw the target line $A-B=L$ in the $(A,B)$ plane. The goal is to find a sequence of lattice points that form a zig-zag path that alternates between lying just above and just below this target line. This defines a sequence of lower and upper approximations. The farther we travel along the target line, the better the approximations become, because the rectangles are shrinking.

It should be geometrically clear how to define the zig-zag path: get as close as you can to the target line as you expand the window in which you search.