3

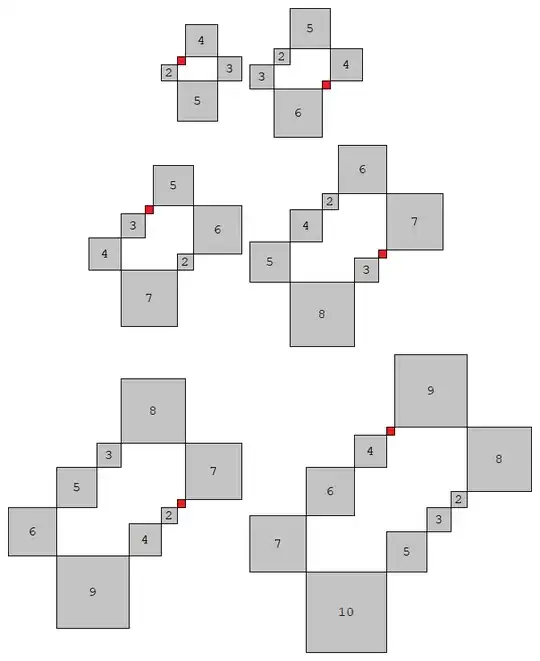
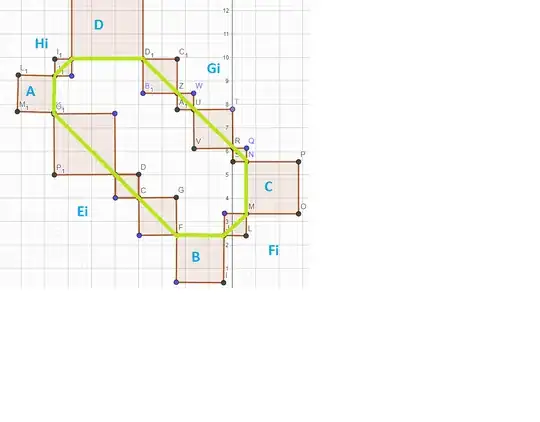
Assume $n$ square bricks with sides $1,2,3,...,n$ where sides of them are parallel to $x,y-$ axis. They are arranged in a pattern in which each brick touches exactly $2$ bricks and two bricks touches such that they have only a vertex common. Prove that $\forall n\geq5$ such arrangement exists?

So, for this problem I tried proving by induction. It's not a big deal to prove such an arrangement willn't possible for $n=1,2,3,4$. So induction follows as,

I've made structure of $n=5$ which is like this,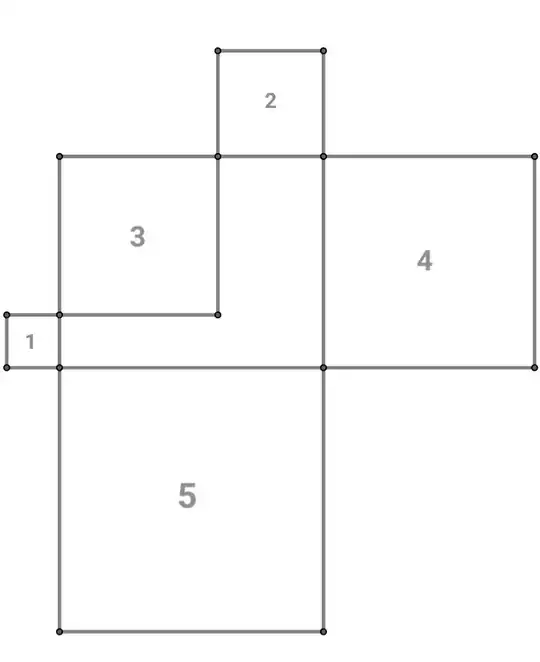enter image description here

Now, I'm unable to get a general conversion from $n=5$ to $n=6$ i.e. $n=i$ to $n=i+1$. Is there a conversion? And what will be the other methods to prove the arrangement to be exist only if $n\geq5$?

Chesx
  • 469

2 Answers2

3

This is almost a proof without words, so I'll let the image speak for itself. What you do with it is up to you.

enter image description here

Daniel Mathias
  • 6,133
0

For any value $n$, we can search for a pattern like this : octogone

A,B,C,D are mandatory. Each group $E_i, F_i, G_i, H_i$ may be empty, or contain 1 or many squares.

So we have to solve :

$\Sigma h_i + d + \Sigma g_i = \Sigma e_i + b + \Sigma f_i$

$\Sigma h_i + a + \Sigma e_i = \Sigma g_i + c + \Sigma f_i$

Probably, the parity of $\frac{n(n+1)}2$ will have an impact at any step.

Lourrran
  • 1,765