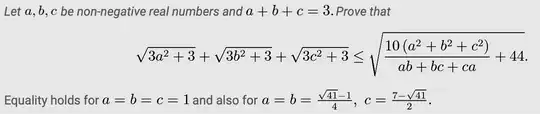From AoPS:
In VMF-er's solution, Ji Chen's lemma was mentioned. I asked VMF-er but have not yet received an answer. Could you please provide me with some information about this theorem? I find it quite interesting. I have searched on AoPS and Stack Exchange but haven't found anything yet. Thank you!
I think it is Lemma 1 below. I discussed it some years ago.
Lemma 1: Let $a, b, c, u, v, w\ge 0$ such that $$a + b + c = u + v + w, \quad ab + bc + ca = uv + vw + wu, \quad abc \ge uvw.$$ Let $f(x)$ be a function with $f'''(x) \ge 0$ on $x \ge 0$. Then $$f(a) + f(b) + f(c) \ge f(u) + f(v) + f(w).$$
$\phantom{2}$
About VMF-er@AoPS's proof:
Let $u = v = 1 + t$ and $w = 1 - 2t$ for $t \le 1/2$. We have $$a + b + c = 3 = u + v + w$$ and $$ab + bc + ca = 3 - 3t^2 = uv + vw + wu.$$ One can prove that $$abc \ge (1 + t)^2(1- 2t) = uvw.$$
Now consider $g(x) = -\sqrt{\frac{x^2 + 1}{2}}$. We have $g'''(x) \ge 0$ on $x \ge 0$. Thus, we have $$g(a) + g(b) + g(c) \ge g(u) + g(v) + g(w) = 2g(1 + t) + g(1 - 2t).$$ The desired result follows.
$\phantom{2}$
About Lemma 1:
https://artofproblemsolving.com/community/c6t321f6h1669330_very_old_one
According to csav10's post, Vasc has posted in 1989, in the Romanian journal Gazeta Matematica A, no. 3, the following lemma which implies Lemma 1.
Lemma 2: Let $f$ is a three differentiable function on interval $I$ and $$a_1 + a_2 + a_3 = c_1 + c_2 + c_3, \quad a_1^2 + a_2^2 + a_3^2 = c_1^2 + c_2^2 + c_3^2$$ where $a_i, c_i\in I$. Then there is $x \in I$ such that $$f(a_1) + f(a_2) + f(a_3) - f(c_1) - f(c_2) - f(c_3) = \frac12(a_1a_2a_3 - c_1c_2c_3) f'''(x).$$
