How can I check that the following subshift of finite type is topologically mixing?

Question

Let me consider the matrix

$$M=\begin{pmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}.$$

I want to prove or disprove if the Markov shift or also called subshift of finite type $S:\Omega_M\rightarrow \Omega_M$ is topologically mixing. Here

$$\Omega_M:=\{\omega\in \Omega| \forall i\in \mathbb{Z}:M(\omega_i,\omega_{i+1})=1\}.$$

I found out that $M$ is irreducible but not aperiodic.

We say that $M$ is irreducible if for all $k,l$ there exists $n\geq1$ such that $M^n(k,l)>0$.

And we say $M$ is aperiodic if there exists $n\geq 1$ such that for all $k,l$ we have $M^n(k,l)>0$.

Now I also know from the lecture that aperiodicity of $M$ implies that $S$ is topologically mixing.

I don't see where to start, can maybe someone help me?

Answer 1

Indeed, the subshift $\sigma:\Omega_M\to \Omega_M$ of finite type defined by the transition matrix $M$ is topologically transitive but not topologically mixing (neither strongly nor weakly; see Topological weakly mixing implies totally transitive for the definitions). Below are two methods to see this.

---

First Method ($\sigma$ is not topologically strong mixing):

First some definitions and preliminaries. Let $A$ be an anonymous $d\times d$ matrix with entries in $\{0,1\}$. Call $A$ irreducible if for any $i,j\in\{1,2,...,d\}$, there is a positive integer $n$ such that $(A^n)_{ij}>0$.

For $i\in\{1,2,...,d\}$, define the period of state $i$ w/r/t $A$ to be

$$\text{period}(i;A)=\gcd\{\ell\in\mathbb{Z}_{\geq1}\,|\, (A^\ell)_{ii}>0\}\in\mathbb{Z}_{\geq1}\cup\{\infty\}.$$

(The period of a state is $\infty$ iff the associated set of returns is empty.)

Next define the period of $A$ to be the greatest common divisor of periods of all those states whose periods are finite.

$$\text{period}(A)=\gcd\{\text{period}(i;A)\,|\, i\in\{1,2,...,d\},\, \text{period}(i;A)<\infty\};$$

if there are no states with finite period then we define the period of $A$ to be infinite.

Here is a useful fact (that we don't really need):

Fact: If $A$ is irreducible, then for any two states $i,j\in\{1,2,...,d\}$ we have that $\text{period}(i;A)=\text{period}(j;A)<\infty$.

As a reference this is Lem.4.5.3 in Lind and Marcus' An Introduction to Symbolic Dynamics and Coding, p.126.

Drawing the diagram associated to $M$ one sees that $M$ has period $2$:

(Alternatively one could argue as coudy.)

Next observe that $\sigma:\Omega_M\to\Omega_M$ being topologically strong mixing implies that $M$ has to be irreducible and of period $1$; indeed irreducibility follows from using cylinder sets defined by the entry at the $0$-th coordinate and "period equals $1$" follows from the infinitude of primes.

(In fact $\sigma:\Omega_M\to\Omega_M$ is topologically strong mixing iff $M$ is irreducible and of period $1$; see Prop.4.5.10 in the aforementioned book, p.129.)

---

Second Method ($\sigma$ is not topologically weak mixing):

For the second method we'll use the fact that topological strong mixing implies topological weak mixing. $\sigma$ being topologically weak mixing is by definition $\sigma\times \sigma:\Omega_M\times\Omega_M\to \Omega_M\times\Omega_M$ being topologically transitive. Products of two subshifts of finite type is a subshift of finite type (over the alphabet that is the product of the alphabets of the factor SFT's). A computation shows that the graph of $\sigma\times \sigma:\Omega_M\times\Omega_M\to \Omega_M\times\Omega_M$ has two connected components; and consequently $\sigma\times \sigma$ is not topologically transitive:

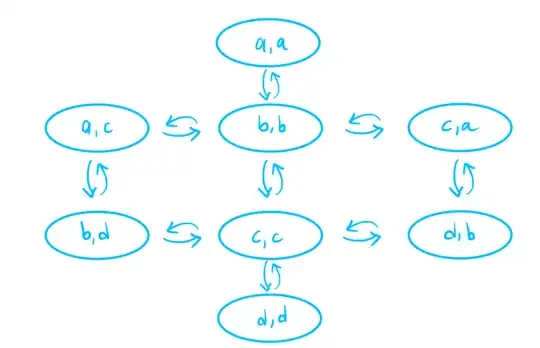
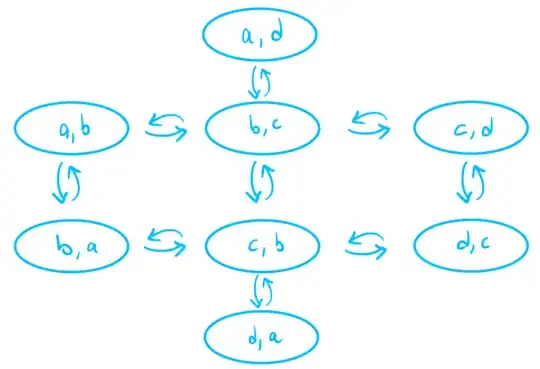
(Through the graph of $\sigma\times\sigma$, choosing an ordering of the $16$ symbols involved, one could also consider the $16\times 16$ adjacency matrix and ask whether or not it is irreducible.)

Answer 2

That subshift is irreducible since any state is connected to any other state, but it is not aperiodic. You can divide the states in two disjoint subsets $\{1,3\}$ and $\{2,4\}$, so that a state in the first set is always followed by a state from the second set, and a state of the second set is always followed by a state from the first set. As a result, $A^{2n}(1,2)$ is zero for all $n$, so is $A^{2n+1}(1,3)$ etc.